Soru Çözümü
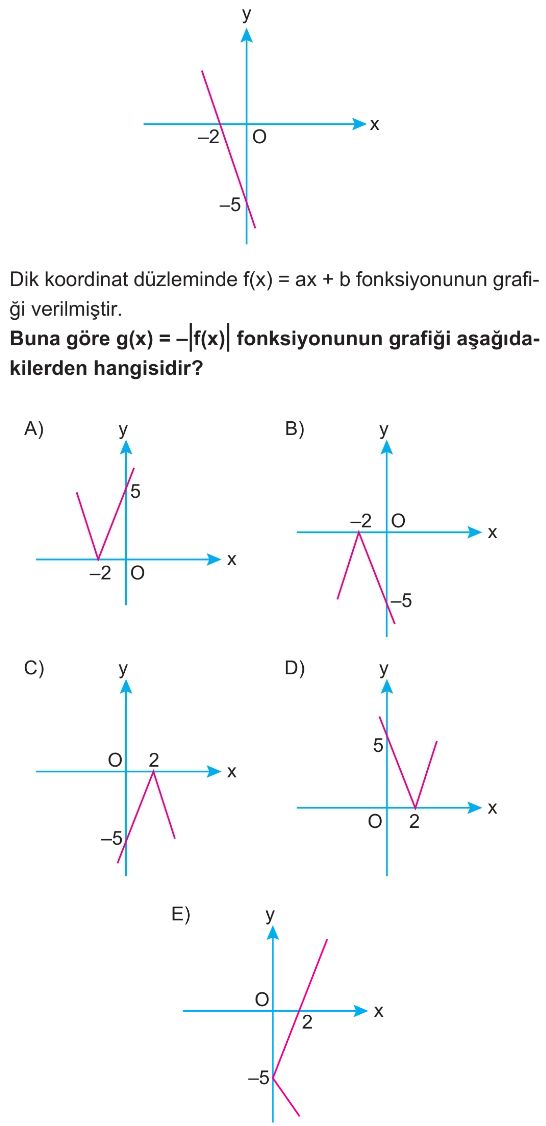
- Verilen $f(x)$ fonksiyonunun grafiği, x eksenini $x=-2$ noktasında ve y eksenini $y=-5$ noktasında kesen bir doğrudur.
- $|f(x)|$ fonksiyonunun grafiğini elde etmek için, $f(x)$'in x ekseninin altında kalan kısımları x eksenine göre yansıtılır. $f(x)$'in $x > -2$ için negatif olan kısmı (örneğin y eksenini kestiği nokta $(0, -5)$) x eksenine göre yansıyarak pozitif olur ve $(0, 5)$ noktasından geçer. $x < -2$ için $f(x)$ pozitif olduğundan bu kısım değişmez. Böylece $|f(x)|$ grafiği $(-2, 0)$ noktasında kırılan ve yukarı doğru açılan bir "V" şeklindedir.
- $g(x) = -|f(x)|$ fonksiyonunun grafiğini elde etmek için, $|f(x)|$ fonksiyonunun grafiği x eksenine göre yansıtılır. Bu, tüm pozitif y değerlerinin negatif olması anlamına gelir.
- $|f(x)|$ grafiğinin kırılma noktası $(-2, 0)$ olduğu için bu nokta x ekseni üzerinde olduğundan yansımadan etkilenmez. $|f(x)|$ grafiği y eksenini $(0, 5)$ noktasında keserken, $-|f(x)|$ grafiği y eksenini $(0, -5)$ noktasında keser.
- Sonuç olarak, $g(x) = -|f(x)|$ grafiği $(-2, 0)$ noktasında kırılan ve aşağı doğru açılan bir "ters V" şeklindedir, y eksenini $(0, -5)$ noktasında keser.
- Bu özelliklere sahip grafik B seçeneğinde gösterilmiştir.
- Doğru Seçenek B'dır.