Soru Çözümü
- Soruda verilen ortalama yağış miktarı $n = 800$ gramdır.
- Fonksiyon $f(x) = |x - n|$ olduğundan, $f(x) = |x - 800|$ olur.
- $x = 800$ için fonksiyon değeri $f(800) = |800 - 800| = |0| = 0$ olur. Bu, grafiğin $(800, 0)$ noktasından geçmesi gerektiğini gösterir.
- En az yağış miktarı $x = 680$ gram için fonksiyon değeri $f(680) = |680 - 800| = |-120| = 120$ olur. Bu, grafiğin $(680, 120)$ noktasından geçmesi gerektiğini gösterir.
- En fazla yağış miktarı $x = 920$ gram için fonksiyon değeri $f(920) = |920 - 800| = |120| = 120$ olur. Bu, grafiğin $(920, 120)$ noktasından geçmesi gerektiğini gösterir.
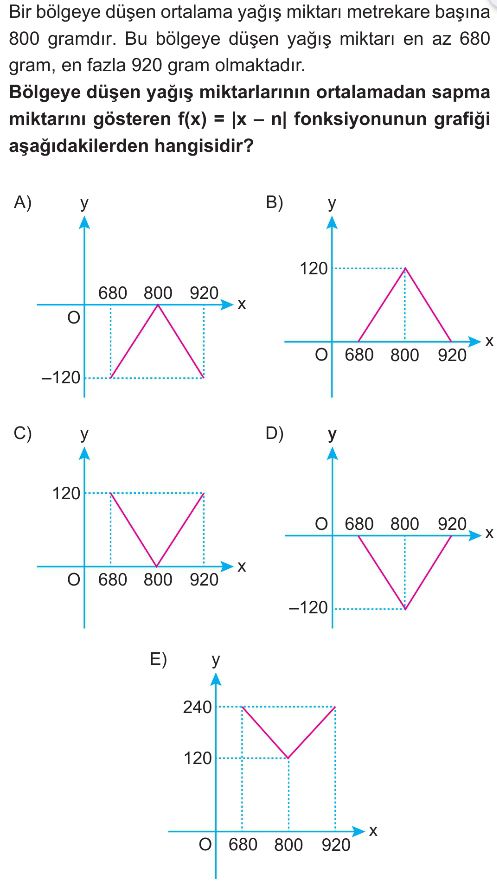
- Bu bilgilere göre, fonksiyonun grafiği $(680, 120)$ noktasından başlayıp $(800, 0)$ noktasına inen ve oradan da $(920, 120)$ noktasına çıkan bir "V" şeklindedir.
- Verilen seçenekler incelendiğinde, C seçeneğindeki grafik bu özellikleri taşımaktadır.
- Doğru Seçenek C'dır.