Soru Çözümü
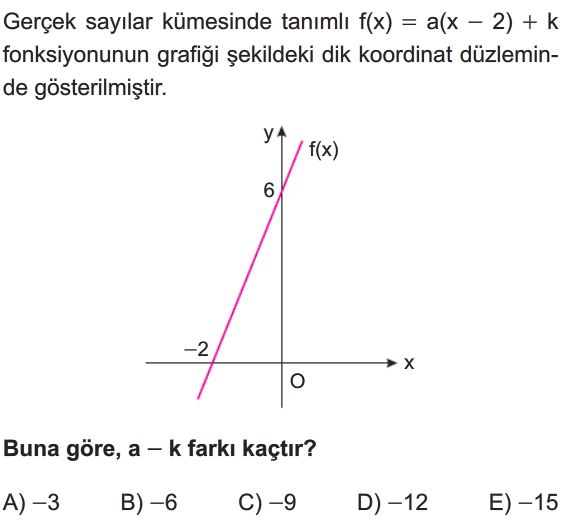
- Grafik, fonksiyonun $(-2, 0)$ noktasından geçtiğini gösterir. Bu noktayı fonksiyonda yerine yazalım: $f(-2) = a(-2 - 2) + k = 0 \Rightarrow a(-4) + k = 0 \Rightarrow -4a + k = 0 \Rightarrow k = 4a$.
- Grafik, fonksiyonun $(0, 6)$ noktasından geçtiğini gösterir. Bu noktayı fonksiyonda yerine yazalım: $f(0) = a(0 - 2) + k = 6 \Rightarrow a(-2) + k = 6 \Rightarrow -2a + k = 6$.
- İlk denklemden bulduğumuz $k = 4a$ ifadesini ikinci denkleme yerine yazalım: $-2a + 4a = 6 \Rightarrow 2a = 6 \Rightarrow a = 3$.
- $a = 3$ değerini $k = 4a$ denkleminde yerine yazarak $k$ değerini bulalım: $k = 4(3) = 12$.
- Son olarak, istenen $a - k$ farkını hesaplayalım: $a - k = 3 - 12 = -9$.
- Doğru Seçenek C'dır.