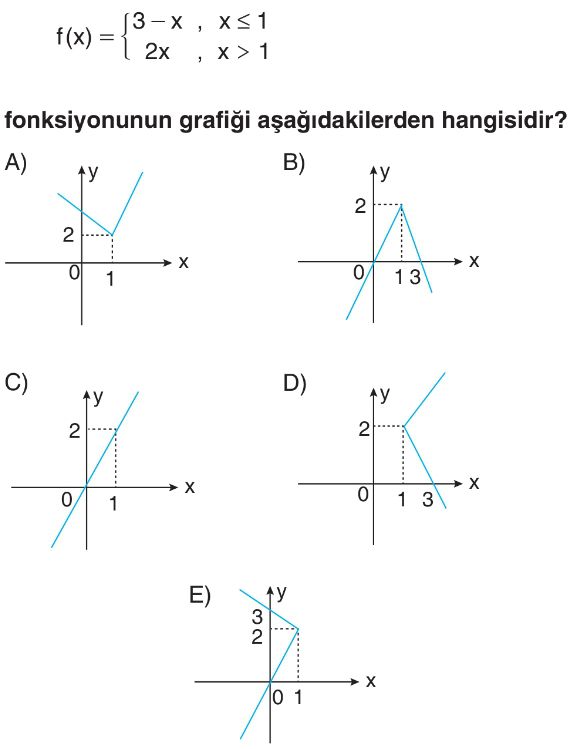
Soru Çözümü
- Verilen fonksiyon iki parçalıdır: $x \le 1$ için $f(x) = 3-x$ ve $x > 1$ için $f(x) = 2x$.
- Birinci parça ($x \le 1$): $f(x) = 3-x$ doğrusunu inceleyelim.
- $x=0$ için $f(0) = 3$. Bu, grafiğin y eksenini $(0, 3)$ noktasında kestiğini gösterir.
- $x=1$ için $f(1) = 3-1 = 2$. Bu, grafiğin $(1, 2)$ noktasından geçtiğini ve bu noktanın dahil olduğunu gösterir.
- İkinci parça ($x > 1$): $f(x) = 2x$ doğrusunu inceleyelim.
- $x=1$ için $f(1)$ değeri $2(1) = 2$ olur. Bu nokta dahil değildir ancak fonksiyon bu noktaya yaklaşır.
- $x > 1$ için $f(x) = 2x$ doğrusu pozitif eğimli, yani yukarı doğru artan bir fonksiyondur. Örneğin $x=2$ için $f(2) = 4$.
- Bu bilgilere göre, grafik $x=1$ noktasında $(1, 2)$ değerini almalı ve bu noktada birleşmelidir. $x \le 1$ için $y=3-x$ doğrusu $(0, 3)$ ve $(1, 2)$ noktalarından geçerken, $x > 1$ için $y=2x$ doğrusu $(1, 2)$ noktasından başlayıp yukarı doğru devam etmelidir.
- Seçenekleri incelediğimizde, A seçeneğindeki grafik bu koşulları tam olarak sağlamaktadır. $(0, 3)$ noktasından başlayıp $(1, 2)$ noktasına gelen ve oradan itibaren $y=2x$ doğrusu şeklinde devam eden bir yapıya sahiptir.
- Diğer seçenekler bu koşulları sağlamaz. Örneğin, B ve C seçeneklerinde $x \le 1$ için grafik $(0,0)$ noktasından geçmektedir, bu da $f(x)=3-x$ ile çelişir.
- Doğru Seçenek A'dır.