Soru Çözümü
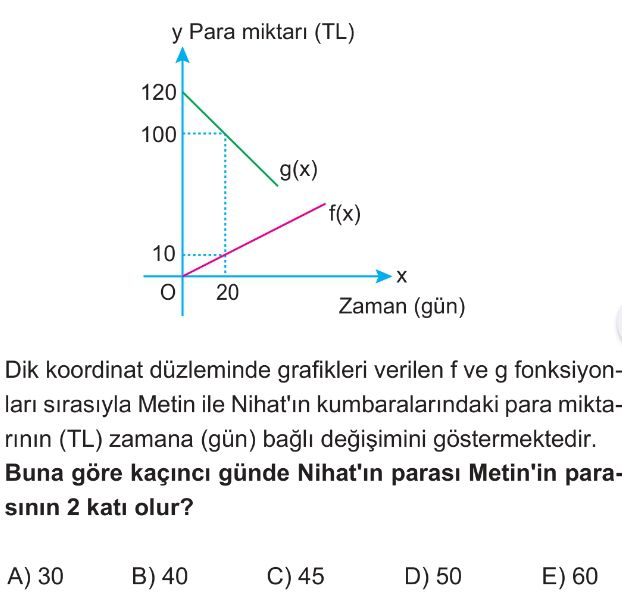
- Metin'in parası (f(x)) için denklemi bulalım. Grafik, $(0,0)$ ve $(20,10)$ noktalarından geçmektedir. Eğim $m_f = \frac{10-0}{20-0} = \frac{1}{2}$'dir. Bu durumda f(x) denklemi $f(x) = \frac{1}{2}x$'dir.
- Nihat'ın parası (g(x)) için denklemi bulalım. Grafik, $(0,120)$ ve $(20,100)$ noktalarından geçmektedir. Eğim $m_g = \frac{100-120}{20-0} = \frac{-20}{20} = -1$'dir. $y$-keseni $120$ olduğundan, g(x) denklemi $g(x) = -x + 120$'dir.
- Nihat'ın parasının Metin'in parasının 2 katı olduğu günü bulmak için $g(x) = 2 \cdot f(x)$ denklemini kuralım.
- Denklemi çözelim: $-x + 120 = 2 \cdot (\frac{1}{2}x)$.
- $-x + 120 = x$.
- $120 = 2x$.
- $x = 60$.
- Doğru Seçenek E'dır.