Soru Çözümü
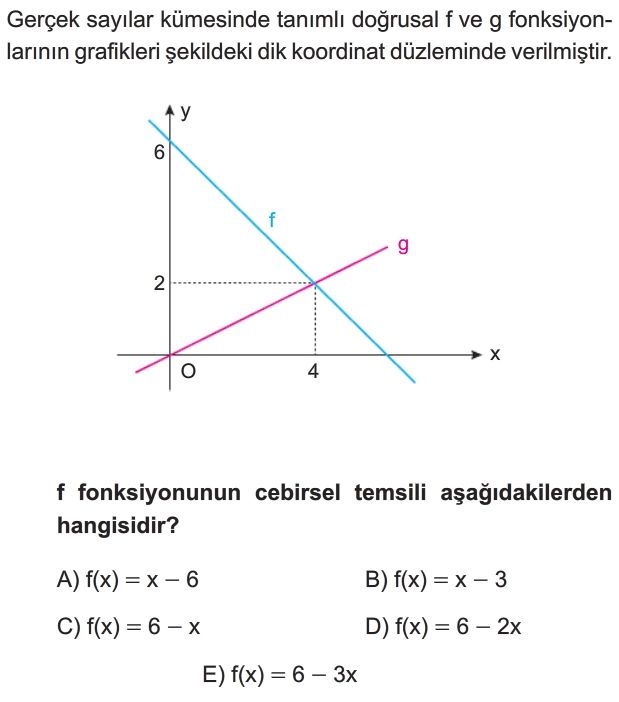
- Grafikteki f fonksiyonunun geçtiği noktaları belirleyelim.
- f fonksiyonu y-eksenini $y = 6$ noktasında kesmektedir, yani bir noktası $(0, 6)$'dır.
- f ve g fonksiyonlarının kesiştiği nokta $(4, 2)$'dir, yani f fonksiyonu $(4, 2)$ noktasından da geçmektedir.
- Doğrusal bir fonksiyonun denklemi $f(x) = mx + b$ şeklindedir.
- Eğimi ($m$) hesaplayalım: $m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{2 - 6}{4 - 0} = \frac{-4}{4} = -1$.
- y-kesen ($b$) değerini belirleyelim: f fonksiyonu y-eksenini $y = 6$ noktasında kestiği için $b = 6$'dır.
- Bu değerleri denklemde yerine koyarak f fonksiyonunun cebirsel temsilini bulalım: $f(x) = -1x + 6 = 6 - x$.
- Doğru Seçenek C'dır.