Soru Çözümü
- Öncelikle, B bitkisinin boyunun $10 cm$ olduğu zamanı bulmak için $y = g(x)$ doğrusunun denklemini belirleyelim.
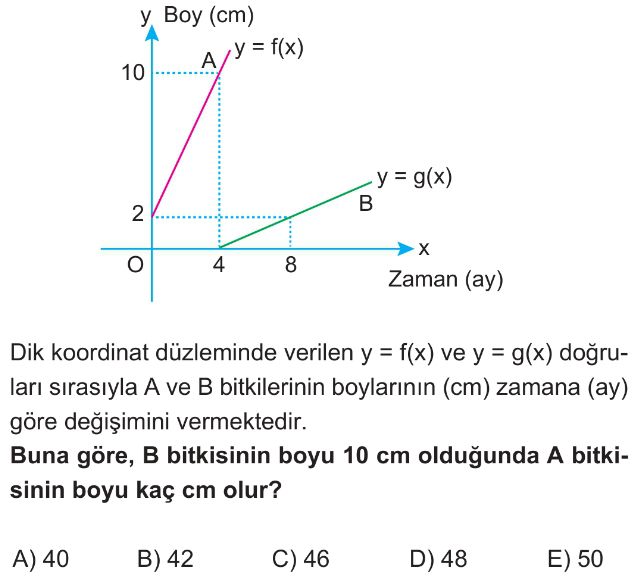
- $g(x)$ doğrusu $(4, 0)$ ve $(8, 2)$ noktalarından geçer. Eğimini hesaplayalım: $m_g = \frac{2 - 0}{8 - 4} = \frac{2}{4} = \frac{1}{2}$.
- Doğrunun denklemi $y - 0 = \frac{1}{2}(x - 4) \Rightarrow g(x) = \frac{1}{2}x - 2$ olur.
- B bitkisinin boyu $10 cm$ olduğunda zamanı bulalım: $10 = \frac{1}{2}x - 2 \Rightarrow 12 = \frac{1}{2}x \Rightarrow x = 24$ ay.
- Şimdi, A bitkisinin boyunu bulmak için $y = f(x)$ doğrusunun denklemini belirleyelim.
- $f(x)$ doğrusu $(0, 2)$ ve $(4, 10)$ noktalarından geçer. Eğimini hesaplayalım: $m_f = \frac{10 - 2}{4 - 0} = \frac{8}{4} = 2$.
- Doğrunun denklemi $y = 2x + 2$ olur (y-keseni $2$'dir).
- A bitkisinin boyunu $x = 24$ ay için hesaplayalım: $f(24) = 2(24) + 2 = 48 + 2 = 50 cm$.
- Doğru Seçenek E'dır.