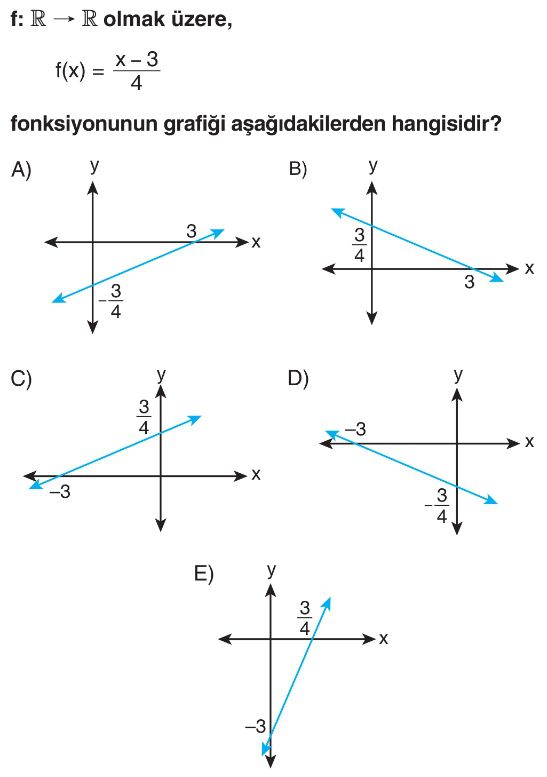
Soru Çözümü
- Verilen fonksiyon $f(x) = \frac{x-3}{4}$ şeklindedir. Bu ifadeyi $y = \frac{x}{4} - \frac{3}{4}$ olarak yazabiliriz.
- Fonksiyonun x eksenini kestiği noktayı bulmak için $y=0$ (veya $f(x)=0$) eşitlenir.
- $0 = \frac{x-3}{4}$ denkleminden $x-3=0$ ve dolayısıyla $x=3$ bulunur. Bu, grafiğin x eksenini $(3, 0)$ noktasında kestiği anlamına gelir.
- Fonksiyonun y eksenini kestiği noktayı bulmak için $x=0$ eşitlenir.
- $f(0) = \frac{0-3}{4} = -\frac{3}{4}$ bulunur. Bu, grafiğin y eksenini $(0, -\frac{3}{4})$ noktasında kestiği anlamına gelir.
- Seçenekler incelendiğinde, A seçeneğindeki grafik x eksenini $3$ noktasında ve y eksenini $-\frac{3}{4}$ noktasında kesmektedir.
- Doğru Seçenek A'dır.