Soru Çözümü
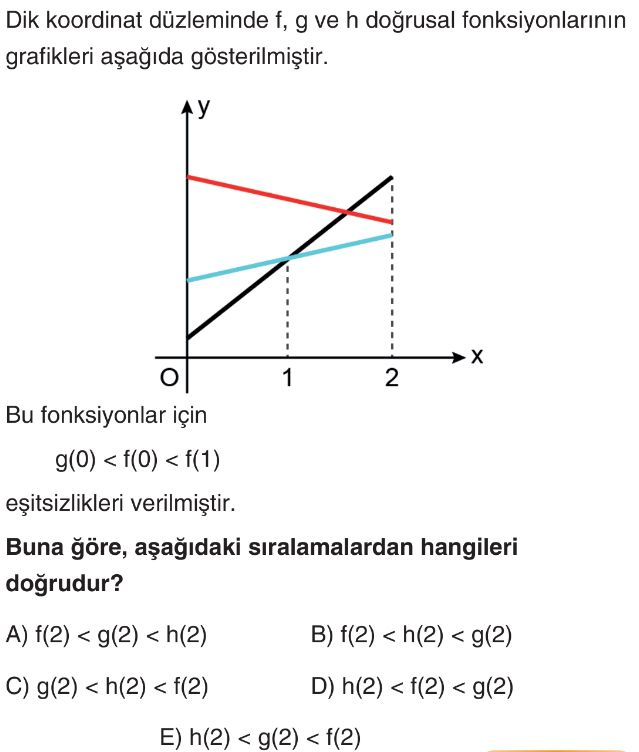
- Grafikteki doğrusal fonksiyonları inceleyelim:
- Siyah çizgi (birinci bölgede artan ve orijinden geçen)
- Kırmızı çizgi (azalan)
- Mavi çizgi (artan, siyah çizgiden daha az eğimli)
- Verilen eşitsizlik $g(0) < f(0) < f(1)$ şeklindedir.
- Grafikten $x=0$ için fonksiyon değerlerine bakalım:
- Siyah çizginin $y$-eksenini kestiği nokta $0$'dır.
- Mavi çizginin $y$-eksenini kestiği nokta pozitif bir değerdir.
- Kırmızı çizginin $y$-eksenini kestiği nokta, mavi çizgiden daha büyük pozitif bir değerdir.
- Bu durumda $g(0)$ en küçük değer olmalıdır, yani $g(0) = 0$. Bu da siyah çizginin $g(x)$ fonksiyonu olduğunu gösterir.
- Şimdi $f(0) < f(1)$ koşuluna bakalım. Bu, $f(x)$ fonksiyonunun artan olduğunu gösterir.
- Kırmızı çizgi azalandır, bu yüzden $f(x)$ olamaz.
- Mavi çizgi artandır. Ayrıca $f(0) > g(0)$ koşulunu sağlar ($f(0) > 0$). Bu yüzden mavi çizgi $f(x)$ fonksiyonudur.
- Geriye kalan kırmızı çizgi ise $h(x)$ fonksiyonudur.
- Şimdi $x=2$ noktasındaki fonksiyon değerlerini grafikten okuyalım:
- $f(2)$ (mavi çizgi) en alttaki değerdir.
- $h(2)$ (kırmızı çizgi) ortadaki değerdir.
- $g(2)$ (siyah çizgi) en üstteki değerdir.
- Bu sıralama $f(2) < h(2) < g(2)$ şeklindedir.
- Doğru Seçenek B'dir.