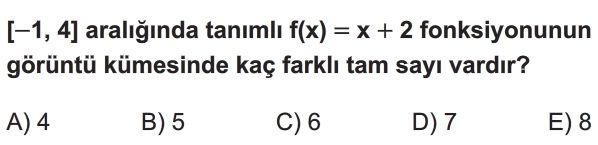
Soru Çözümü
- Verilen fonksiyon $f(x) = x + 2$'dir ve tanım aralığı $[-1, 4]$'tür. Bu, $-1 \le x \le 4$ anlamına gelir.
- Görüntü kümesini bulmak için tanım aralığının uç noktalarını fonksiyonda yerine koyarız.
- $x = -1$ için $f(-1) = -1 + 2 = 1$ olur.
- $x = 4$ için $f(4) = 4 + 2 = 6$ olur.
- Fonksiyon $f(x) = x + 2$ artandır, bu nedenle görüntü kümesi $[1, 6]$ aralığıdır. Yani $1 \le f(x) \le 6$.
- Bu aralıktaki tam sayılar $1, 2, 3, 4, 5, 6$'dır.
- Toplamda $6$ farklı tam sayı vardır.
- Doğru Seçenek C'dır.