Soru Çözümü
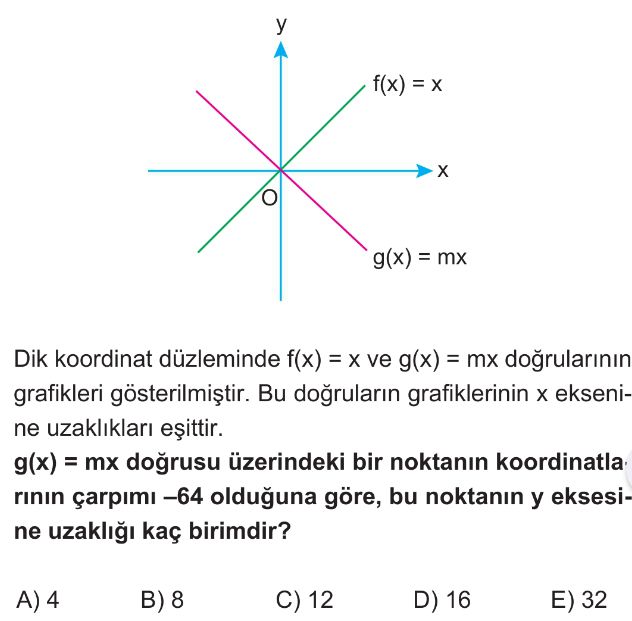
- $f(x) = x$ doğrusunun eğimi $1$'dir.
- Doğruların x eksenine uzaklıklarının eşit olması, eğimlerinin mutlak değerlerinin eşit olduğu anlamına gelir.
- Grafikte $g(x) = mx$ doğrusu ikinci ve dördüncü bölgelerden geçtiği için eğimi $m$ negatiftir.
- Bu durumda $m = -1$ olmalıdır. Yani $g(x) = -x$ doğrusudur.
- $g(x)$ doğrusu üzerindeki bir nokta $(x, y)$ olsun. Bu noktanın koordinatları çarpımı $x \cdot y = -64$ olarak verilmiştir.
- $y = -x$ olduğundan, $x \cdot (-x) = -64$ denklemini çözeriz.
- $-x^2 = -64 \Rightarrow x^2 = 64$ olur.
- Buradan $x = 8$ veya $x = -8$ bulunur.
- Bir noktanın y eksenine uzaklığı, o noktanın apsisinin mutlak değeri ($|x|$) ile bulunur.
- Her iki durumda da uzaklık $|8| = 8$ birim veya $|-8| = 8$ birimdir.
- Doğru Seçenek B'dır.