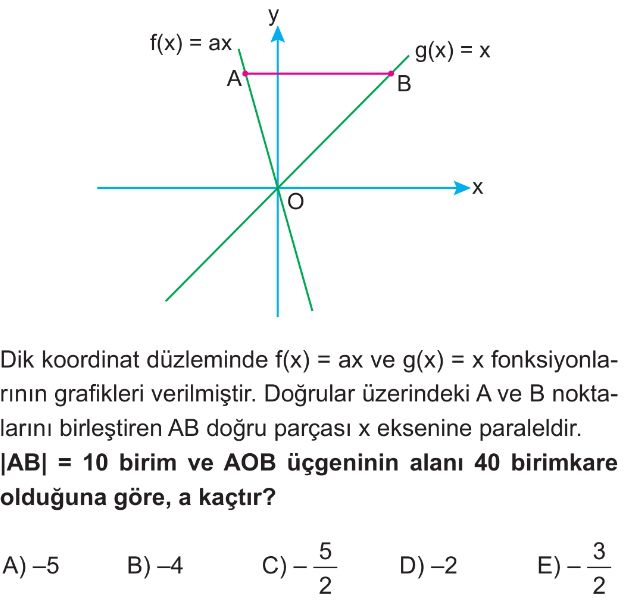
Soru Çözümü
- AB doğru parçası x eksenine paralel olduğundan, A ve B noktalarının y koordinatları eşittir. Bu ortak y koordinatına $h$ diyelim.
- A noktası $f(x) = ax$ üzerinde olduğundan, $A(x_A, h)$ için $h = ax_A \implies x_A = h/a$.
- B noktası $g(x) = x$ üzerinde olduğundan, $B(x_B, h)$ için $h = x_B$.
- AOB üçgeninin tabanı AB doğru parçasıdır ve uzunluğu $|AB| = 10$ birimdir.
- AOB üçgeninin yüksekliği, O noktasının AB doğrusuna olan uzaklığıdır. AB doğrusu $y=h$ olduğundan, yükseklik $h$ birimdir (grafikten $h>0$ olduğu görülür).
- AOB üçgeninin alanı $(1/2) \times \text{taban} \times \text{yükseklik}$ formülüyle bulunur. Verilen alan $40$ birimkaredir.
- $40 = (1/2) \times 10 \times h \implies 40 = 5h \implies h = 8$.
- Şimdi A ve B noktalarının koordinatları $A(8/a, 8)$ ve $B(8, 8)$ olur.
- $|AB| = |x_B - x_A|$ olduğundan, $10 = |8 - 8/a|$. Grafikten $x_B > x_A$ olduğu için $10 = 8 - 8/a$.
- $10 - 8 = -8/a \implies 2 = -8/a$.
- $2a = -8 \implies a = -4$.
- Doğru Seçenek B'dır.