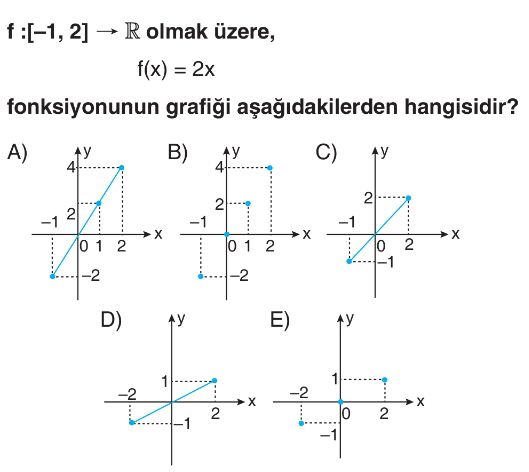
Soru Çözümü
- Verilen fonksiyon $f:[-1, 2] \rightarrow \mathbb{R}$, $f(x) = 2x$'tir.
- Fonksiyonun tanım kümesi $[-1, 2]$ olduğundan, $x$ değerleri $-1$ ile $2$ arasındadır ve bu değerler de dahildir.
- Tanım kümesinin başlangıç noktası için $x = -1$ değerini fonksiyonda yerine koyalım: $f(-1) = 2(-1) = -2$. Bu, grafiğin $(-1, -2)$ noktasından başlaması gerektiğini gösterir.
- Tanım kümesinin bitiş noktası için $x = 2$ değerini fonksiyonda yerine koyalım: $f(2) = 2(2) = 4$. Bu, grafiğin $(2, 4)$ noktasında bitmesi gerektiğini gösterir.
- $f(x) = 2x$ bir doğrusal fonksiyondur, bu yüzden grafiği $(-1, -2)$ ve $(2, 4)$ noktalarını birleştiren bir doğru parçası olmalıdır.
- Seçenekler incelendiğinde, A seçeneğindeki grafik $(-1, -2)$ noktasından başlayıp $(2, 4)$ noktasında biten bir doğru parçasını göstermektedir.
- Diğer seçenekler, ya farklı başlangıç/bitiş noktalarına sahiptir ya da doğrusal bir fonksiyonu temsil etmemektedir.
- Doğru Seçenek A'dır.