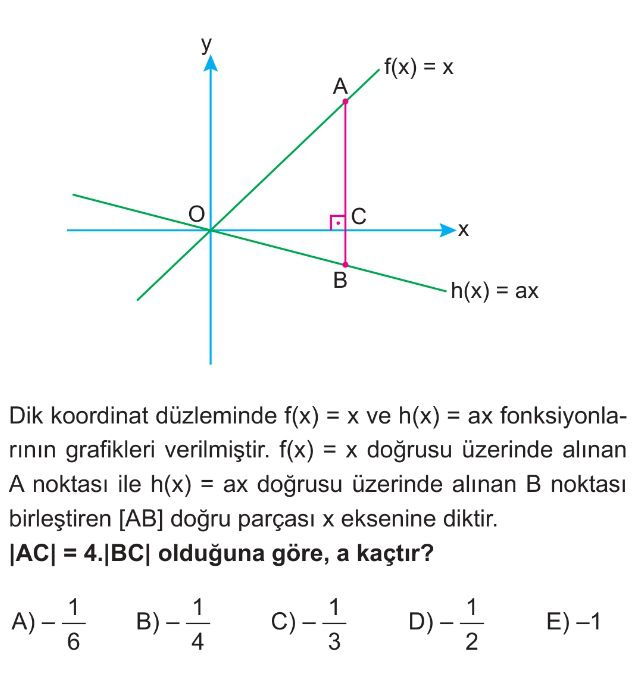
Soru Çözümü
- A noktasının koordinatları $f(x) = x$ üzerinde olduğundan $A(x_0, x_0)$ olarak alınır.
- B noktasının koordinatları $h(x) = ax$ üzerinde olduğundan $B(x_0, ax_0)$ olarak alınır.
- [AB] doğru parçası x eksenine dik olduğundan, C noktası A ve B'nin x ekseni üzerindeki izdüşümüdür. Bu durumda $C(x_0, 0)$ olur.
- $|AC|$ uzunluğu, A noktasının y-koordinatının mutlak değeridir: $|AC| = |x_0 - 0| = x_0$. (Şekle göre $x_0 > 0$)
- $|BC|$ uzunluğu, B noktasının y-koordinatının mutlak değeridir: $|BC| = |ax_0 - 0| = |ax_0|$. (Şekle göre B noktası x ekseninin altında olduğundan $ax_0 < 0$, dolayısıyla $|ax_0| = -ax_0$ olur.)
- Verilen $|AC| = 4 \cdot |BC|$ eşitliğini yerine yazarsak: $x_0 = 4 \cdot (-ax_0)$.
- Eşitliğin her iki tarafını $x_0$ ile böleriz (çünkü $x_0 \neq 0$): $1 = -4a$.
- Buradan $a = -\frac{1}{4}$ bulunur.
- Doğru Seçenek B'dır.