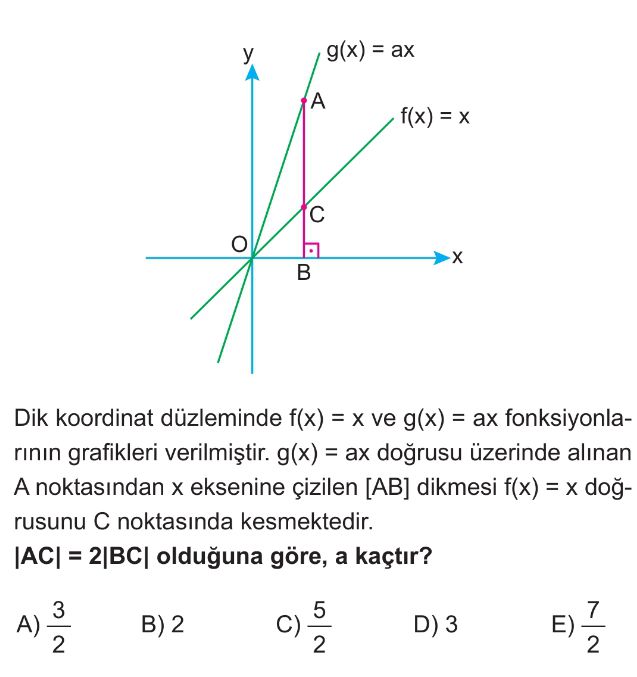
Soru Çözümü
- B noktasının x koordinatı $x_0$ olsun. O zaman $B = (x_0, 0)$ olur.
- A noktası $g(x) = ax$ doğrusu üzerinde ve x koordinatı $x_0$ olduğundan $A = (x_0, ax_0)$ olur.
- C noktası $f(x) = x$ doğrusu üzerinde ve x koordinatı $x_0$ olduğundan $C = (x_0, x_0)$ olur.
- $|AC|$ uzunluğu, A ve C noktalarının y koordinatları farkıdır: $|AC| = ax_0 - x_0 = (a-1)x_0$. (Şekle göre $ax_0 > x_0$)
- $|BC|$ uzunluğu, C ve B noktalarının y koordinatları farkıdır: $|BC| = x_0 - 0 = x_0$.
- Soruda verilen $|AC| = 2|BC|$ eşitliğini kullanalım: $(a-1)x_0 = 2x_0$.
- $x_0 \ne 0$ olduğu için her iki tarafı $x_0$ ile bölebiliriz: $a-1 = 2$.
- Buradan $a = 2+1 = 3$ bulunur.
- Doğru Seçenek D'dır.