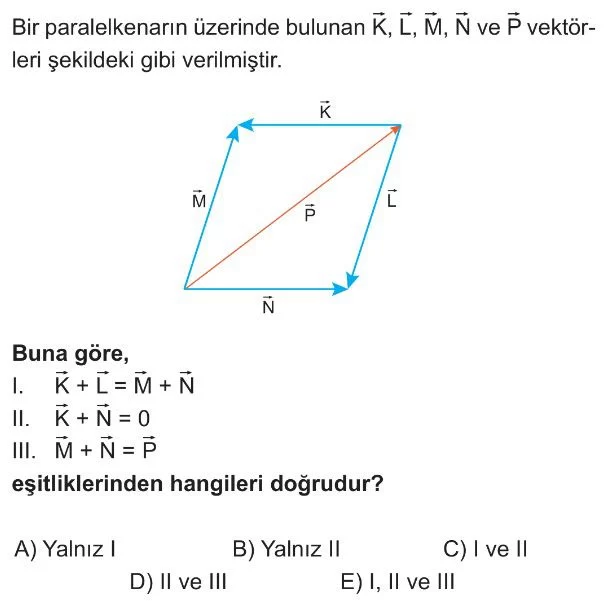
Soru Çözümü
- Paralelkenarın özelliklerine göre, karşılıklı kenarları temsil eden vektörler eşit büyüklükte ve zıt yönlüdür. Bu durumda $\vec{K} = -\vec{N}$ ve $\vec{M} = -\vec{L}$ olur.
- I. öncülü inceleyelim: $\vec{K} + \vec{L} = \vec{M} + \vec{N}$.
- $\vec{K}$ yerine $-\vec{N}$ ve $\vec{L}$ yerine $-\vec{M}$ yazarsak: $(-\vec{N}) + (-\vec{M}) = \vec{M} + \vec{N}$ ifadesini elde ederiz.
- Bu ifade $-\vec{N} - \vec{M} = \vec{M} + \vec{N}$ şeklini alır. Bu eşitlik yanlıştır.
- II. öncülü inceleyelim: $\vec{K} + \vec{N} = \vec{0}$.
- Yukarıda belirttiğimiz gibi $\vec{K} = -\vec{N}$ olduğundan, $\vec{K} + \vec{N} = (-\vec{N}) + \vec{N} = \vec{0}$ eşitliği doğrudur.
- III. öncülü inceleyelim: $\vec{M} + \vec{N} = \vec{P}$.
- Vektörlerde paralelkenar kuralına göre, aynı noktadan başlayan iki vektörün ($\vec{M}$ ve $\vec{N}$) toplamı, bu vektörlerin oluşturduğu paralelkenarın aynı noktadan çıkan köşegen vektörüne ($\vec{P}$) eşittir. Şekilde bu durum açıkça gösterilmiştir. Bu eşitlik doğrudur.
- Buna göre, II ve III numaralı öncüller doğrudur.
- Doğru Seçenek D'dır.