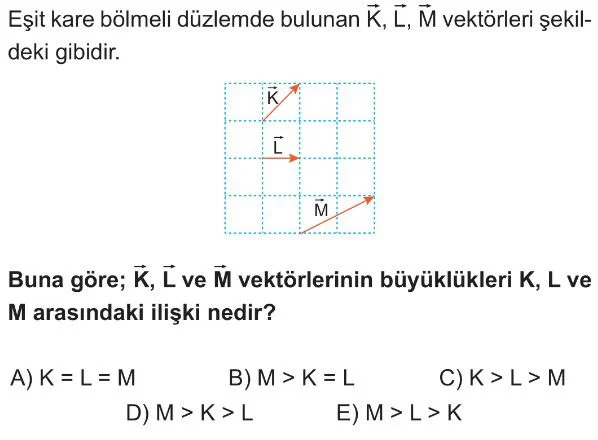
Soru Çözümü
- Her bir kare kenarının uzunluğunu $1$ birim kabul edelim.
- K vektörünün büyüklüğü: Yatay bileşen $2$ birim, düşey bileşen $1$ birimdir. Pisagor teoreminden $K = \sqrt{2^2 + 1^2} = \sqrt{5}$ bulunur.
- L vektörünün büyüklüğü: Yatay bileşen $2$ birim, düşey bileşen $0$ birimdir. $L = \sqrt{2^2 + 0^2} = \sqrt{4} = 2$ bulunur.
- M vektörünün büyüklüğü: Yatay bileşen $3$ birim, düşey bileşen $1$ birimdir. Pisagor teoreminden $M = \sqrt{3^2 + 1^2} = \sqrt{10}$ bulunur.
- Büyüklükleri karşılaştırırsak: $M = \sqrt{10} \approx 3.16$, $K = \sqrt{5} \approx 2.24$, $L = 2$.
- Bu durumda büyüklükler arasındaki ilişki $M > K > L$ şeklindedir.
- Doğru Seçenek D'dır.