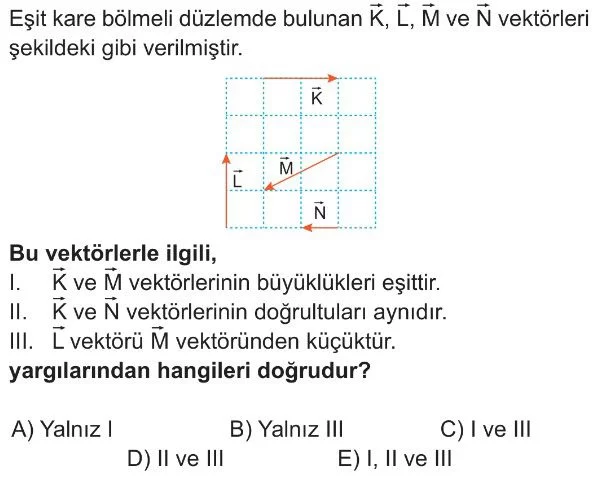
Soru Çözümü
- Vektörlerin büyüklüklerini belirleyelim (birim kare kenarı $1$ birim kabul edilirse):
- $|\vec{K}| = 2$ birim
- $|\vec{L}| = 1$ birim
- $|\vec{M}| = \sqrt{1^2 + 1^2} = \sqrt{2}$ birim
- $|\vec{N}| = 2$ birim
- I. K ve M vektörlerinin büyüklükleri eşittir.
- $|\vec{K}| = 2$ birim ve $|\vec{M}| = \sqrt{2}$ birimdir. $2 \neq \sqrt{2}$ olduğundan bu ifade yanlıştır.
- II. K ve N vektörlerinin doğrultuları aynıdır.
- $\vec{K}$ vektörü yatay doğrultuda (sağa), $\vec{N}$ vektörü de yatay doğrultudadır (sola). Yönleri farklı olsa da doğrultuları (yatay) aynıdır. Bu ifade doğrudur.
- III. L vektörü M vektöründen küçüktür.
- $|\vec{L}| = 1$ birim ve $|\vec{M}| = \sqrt{2} \approx 1.414$ birimdir. $1 < \sqrt{2}$ olduğundan $|\vec{L}| < |\vec{M}|$ ifadesi doğrudur.
- Doğru olan yargılar II ve III'tür.
- Doğru Seçenek D'dır.