Soru Çözümü
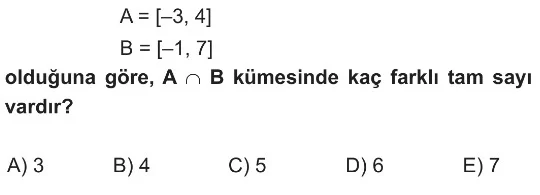
- Verilen kümeler kapalı aralıklar şeklindedir: $A = [-3, 4]$ ve $B = [-1, 7]$.
- Bu aralıklar sırasıyla $-3 \le x \le 4$ ve $-1 \le x \le 7$ eşitsizliklerini ifade eder.
- $A \cap B$ kümesini bulmak için her iki eşitsizliği de sağlayan ortak aralığı belirlemeliyiz.
- $A \cap B$ aralığı, başlangıç noktalarının en büyüğü ve bitiş noktalarının en küçüğü alınarak bulunur.
- Başlangıç noktaları $-3$ ve $-1$'dir. Bunların en büyüğü $\max(-3, -1) = -1$'dir.
- Bitiş noktaları $4$ ve $7$'dir. Bunların en küçüğü $\min(4, 7) = 4$'tür.
- Bu durumda $A \cap B = [-1, 4]$ olur.
- $[-1, 4]$ aralığındaki tam sayılar $-1, 0, 1, 2, 3, 4$'tür.
- Bu aralıktaki tam sayıların sayısı $4 - (-1) + 1 = 4 + 1 + 1 = 6$'dır.
- Doğru Seçenek D'dır.