Soru Çözümü
- I. ifadeyi kontrol edelim: $A \cap B = B$
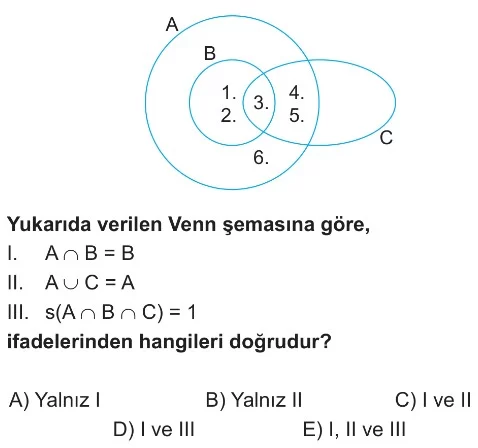
- Venn şemasına göre, B kümesi tamamen A kümesinin içindedir ($B \subseteq A$).
- Bu durumda, A ve B kümelerinin kesişimi B kümesinin kendisidir. Yani $A \cap B = \{1, 2, 3\} = B$.
- Bu ifade doğrudur.
- II. ifadeyi kontrol edelim: $A \cup C = A$
- Venn şemasına göre, C kümesinin tüm elemanları A kümesinin içindedir ($C \subseteq A$).
- Bir küme başka bir kümenin alt kümesi olduğunda, birleşimleri büyük kümeyi verir. Yani $A \cup C = \{1, 2, 3, 4, 5, 6\} \cup \{3, 4, 5\} = \{1, 2, 3, 4, 5, 6\} = A$.
- Bu ifade doğrudur.
- III. ifadeyi kontrol edelim: $s(A \cap B \cap C) = 1$
- $A \cap B \cap C$ ifadesi, A, B ve C kümelerinin üçünün de ortak elemanlarını gösterir.
- Venn şemasında üç kümenin kesiştiği bölge sadece '3' numarasını içerir. Yani $A \cap B \cap C = \{3\}$.
- Bu kümenin eleman sayısı $s(A \cap B \cap C) = 1$'dir.
- Bu ifade doğrudur.
- Tüm ifadeler (I, II ve III) doğru olduğu için, doğru seçenek E'dir.