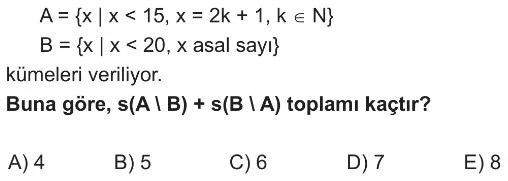
Soru Çözümü
- Öncelikle A kümesinin elemanlarını belirleyelim. Verilen $A = \{x \mid x < 15, x = 2k + 1, k \in \mathbb{N}\}$ ifadesinde $k \in \mathbb{N}$ (doğal sayılar, $0, 1, 2, \dots$) ve $x < 15$ koşullarıyla, $A$ kümesi 15'ten küçük tek doğal sayılardan oluşur. $A = \{1, 3, 5, 7, 9, 11, 13\}$
- Şimdi B kümesinin elemanlarını belirleyelim. Verilen $B = \{x \mid x < 20, x \text{ asal sayı}\}$ ifadesinde $x < 20$ koşuluyla, $B$ kümesi 20'den küçük asal sayılardan oluşur. $B = \{2, 3, 5, 7, 11, 13, 17, 19\}$
- $A \setminus B$ kümesi, A kümesinde olup B kümesinde olmayan elemanlardır. $A \setminus B = \{1, 9\}$ Bu kümenin eleman sayısı $s(A \setminus B) = 2$
- $B \setminus A$ kümesi, B kümesinde olup A kümesinde olmayan elemanlardır. $B \setminus A = \{2, 17, 19\}$ Bu kümenin eleman sayısı $s(B \setminus A) = 3$
- Son olarak, istenen toplamı hesaplayalım: $s(A \setminus B) + s(B \setminus A) = 2 + 3 = 5$
- Doğru Seçenek B'dır.