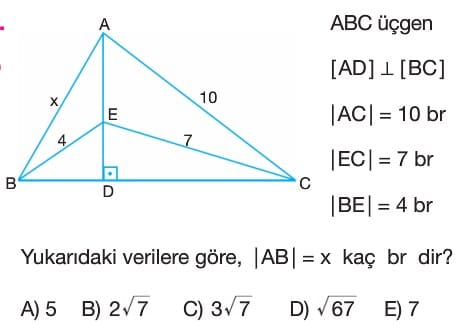
Soru Çözümü
- EBD üçgeninde Pisagor teoremini uygulayalım: $|BE|^2 = |ED|^2 + |BD|^2 \implies 4^2 = |ED|^2 + |BD|^2 \implies 16 = |ED|^2 + |BD|^2$.
- ECD üçgeninde Pisagor teoremini uygulayalım: $|EC|^2 = |ED|^2 + |CD|^2 \implies 7^2 = |ED|^2 + |CD|^2 \implies 49 = |ED|^2 + |CD|^2$.
- İkinci denklemden birinci denklemi çıkaralım: $49 - 16 = (|ED|^2 + |CD|^2) - (|ED|^2 + |BD|^2) \implies 33 = |CD|^2 - |BD|^2$.
- ABD üçgeninde Pisagor teoremini uygulayalım: $|AB|^2 = |AD|^2 + |BD|^2 \implies x^2 = |AD|^2 + |BD|^2$.
- ACD üçgeninde Pisagor teoremini uygulayalım: $|AC|^2 = |AD|^2 + |CD|^2 \implies 10^2 = |AD|^2 + |CD|^2 \implies 100 = |AD|^2 + |CD|^2$.
- Beşinci denklemden dördüncü denklemi çıkaralım: $100 - x^2 = (|AD|^2 + |CD|^2) - (|AD|^2 + |BD|^2) \implies 100 - x^2 = |CD|^2 - |BD|^2$.
- Üçüncü ve altıncı denklemleri eşitleyelim: $33 = 100 - x^2 \implies x^2 = 100 - 33 \implies x^2 = 67 \implies x = \sqrt{67}$ br.
- Doğru Seçenek D'dır.