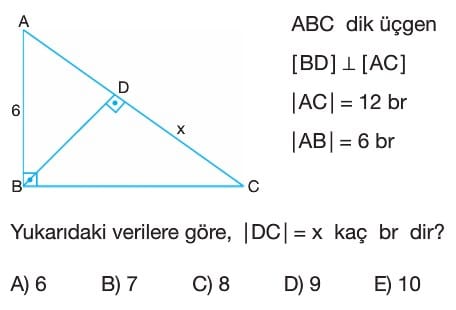
Soru Çözümü
- ABC dik üçgeninde, B köşesinden hipotenüs AC'ye indirilen BD dikmesi Öklid bağıntılarını sağlar.
- Öklid bağıntılarından birine göre, bir dik kenarın karesi, hipotenüs ile o dik kenarın hipotenüs üzerindeki iz düşümünün çarpımına eşittir.
- AB kenarı için bu bağıntı: $|AB|^2 = |AD| \cdot |AC|$ şeklinde ifade edilir.
- Verilen değerleri yerine yazalım: $|AB| = 6$ br ve $|AC| = 12$ br.
- Denklem `$6^2 = |AD| \cdot 12$` olur.
- Bu denklemi çözdüğümüzde `$36 = 12 \cdot |AD|$` elde ederiz.
- Buradan `$|AD| = \frac{36}{12} = 3$ br` bulunur.
- Hipotenüsün tamamı `$|AC| = |AD| + |DC|$` olduğundan, `$12 = 3 + x$` yazabiliriz.
- Denklemi çözerek `$x = 12 - 3 = 9$ br` sonucuna ulaşırız.
- Doğru Seçenek D'dır.