Soru Çözümü
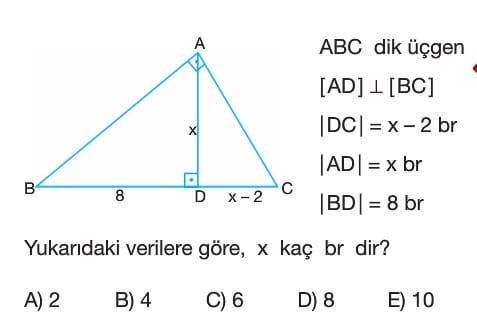
- ABC dik üçgeninde, hipotenüse ait yükseklik için Öklid Bağıntısı kullanılır.
- Öklid Bağıntısı'na göre, yüksekliğin karesi, hipotenüs üzerinde ayırdığı parçaların çarpımına eşittir: $|AD|^2 = |BD| \cdot |DC|$.
- Verilen değerleri yerine yazalım: $x^2 = 8 \cdot (x - 2)$.
- Denklemi düzenleyelim: $x^2 = 8x - 16$.
- Denklemi bir tarafa toplayalım: $x^2 - 8x + 16 = 0$.
- Bu ifade bir tam kare denklemdir: $(x - 4)^2 = 0$.
- Denklemden $x$ değerini bulalım: $x - 4 = 0 \Rightarrow x = 4$.
- $|DC|$ uzunluğu pozitif olmalıdır ($x - 2 > 0$). $4 - 2 = 2 > 0$ olduğu için $x=4$ değeri geçerlidir.
- Doğru Seçenek B'dır.