Soru Çözümü
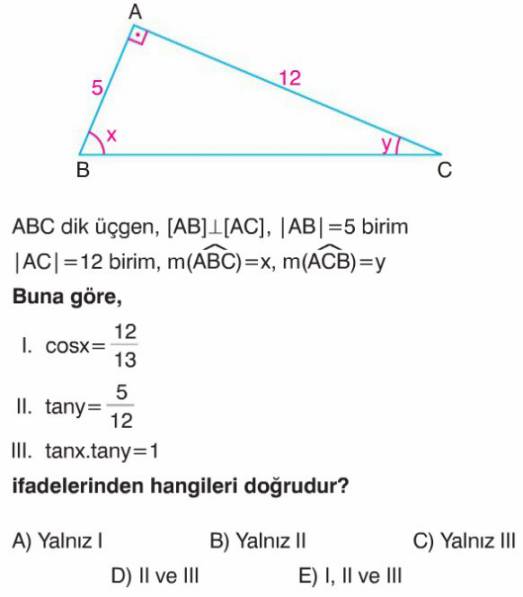
- ABC dik üçgeninde Pisagor teoremini kullanarak hipotenüs uzunluğunu bulalım: $|BC|^2 = |AB|^2 + |AC|^2 = 5^2 + 12^2 = 25 + 144 = 169$. Böylece $|BC| = \sqrt{169} = 13$ birimdir.
- I. ifadeyi inceleyelim: $\cos x = \frac{\text{komşu kenar}}{\text{hipotenüs}}$. B açısı ($x$) için komşu kenar $|AB|=5$, hipotenüs $|BC|=13$ olduğundan $\cos x = \frac{5}{13}$ olmalıdır. Verilen ifade $\cos x = \frac{12}{13}$ olduğu için I. ifade yanlıştır.
- II. ifadeyi inceleyelim: $\tan y = \frac{\text{karşı kenar}}{\text{komşu kenar}}$. C açısı ($y$) için karşı kenar $|AB|=5$, komşu kenar $|AC|=12$ olduğundan $\tan y = \frac{5}{12}$ olmalıdır. Verilen ifade $\tan y = \frac{5}{12}$ olduğu için II. ifade doğrudur.
- III. ifadeyi inceleyelim: $\tan x \cdot \tan y = 1$.
- B açısı ($x$) için $\tan x = \frac{\text{karşı kenar}}{\text{komşu kenar}} = \frac{|AC|}{|AB|} = \frac{12}{5}$'tir.
- C açısı ($y$) için $\tan y = \frac{5}{12}$ olduğunu II. maddede bulmuştuk.
- Çarpımlarını hesaplayalım: $\tan x \cdot \tan y = \frac{12}{5} \cdot \frac{5}{12} = 1$.
- Alternatif olarak, bir dik üçgende dik açının dışındaki diğer iki açının toplamı $90^\circ$ olduğundan $x+y=90^\circ$'dir. Bu durumda $\tan x = \cot y$ olur. Dolayısıyla $\tan x \cdot \tan y = \cot y \cdot \tan y = 1$'dir.
- Doğru olan ifadeler II ve III'tür.
- Doğru Seçenek D'dır.