Soru Çözümü
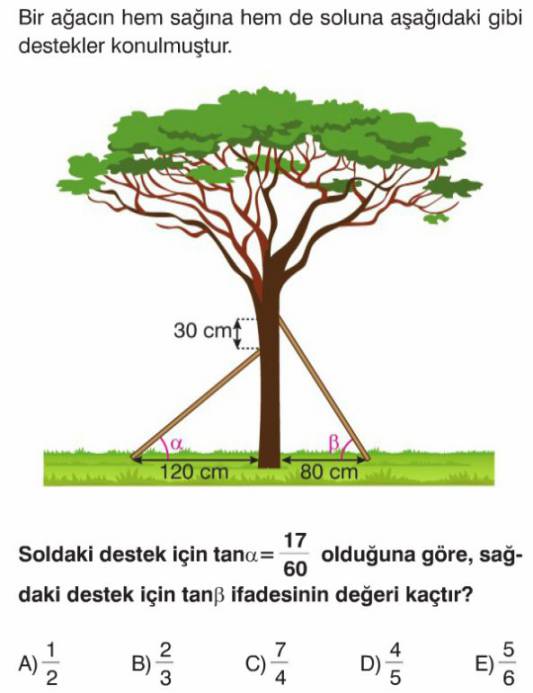
- Sol taraftaki destek için oluşan dik üçgende, yüksekliği $h_L$ ve taban uzunluğunu $120 cm$ olarak alalım.
- Verilen $tan\alpha$ değerini kullanarak $h_L$ yüksekliğini hesaplayalım:
$tan\alpha = \frac{h_L}{120 cm} = \frac{17}{60}$
$h_L = \frac{17}{60} \times 120 cm = 17 \times 2 cm = 34 cm$. - Şekildeki $30 cm$ uzunluğu, sol destekteki bağlantı noktasından yukarıya doğru olan dikey mesafeyi göstermektedir. Bu, sağ destekteki bağlantı noktasının yüksekliğinin ($h_R$) sol destekteki bağlantı noktasının yüksekliğinden ($h_L$) $30 cm$ daha fazla olduğunu ifade eder.
$h_R = h_L + 30 cm = 34 cm + 30 cm = 64 cm$. - Sağ taraftaki destek için oluşan dik üçgende, yüksekliği $h_R = 64 cm$ ve taban uzunluğunu $80 cm$ olarak alalım. Şimdi $tan\beta$ değerini hesaplayalım:
$tan\beta = \frac{h_R}{80 cm} = \frac{64 cm}{80 cm}$
$tan\beta = \frac{64}{80}$. - Kesri sadeleştirelim (her iki tarafı 16'ya bölerek):
$tan\beta = \frac{4}{5}$. - Doğru Seçenek D'dır.