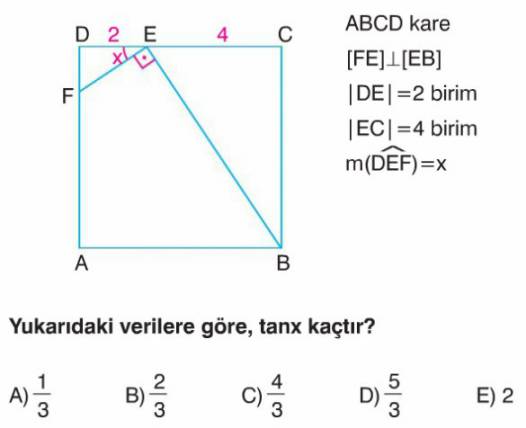
Soru Çözümü
- ABCD kare olduğundan, tüm kenar uzunlukları eşittir. $|DC| = |DE| + |EC| = 2 + 4 = 6$ birimdir. Bu durumda $|AD| = |BC| = 6$ birimdir.
- $D, E, C$ noktaları doğrusal olduğundan $m(\angle DEC) = 180^\circ$ bir doğru açıdır.
- Verilen $m(\angle FEB) = 90^\circ$ olduğundan, $m(\angle DEF) + m(\angle BEC) = 180^\circ - 90^\circ = 90^\circ$ olur.
- $m(\angle DEF) = x$ olarak verildiğinden, $x + m(\angle BEC) = 90^\circ$ ve dolayısıyla $m(\angle BEC) = 90^\circ - x$ olur.
- $\triangle EBC$ bir dik üçgendir ($m(\angle C) = 90^\circ$). Bu üçgende $m(\angle CBE) = 180^\circ - 90^\circ - m(\angle BEC) = 90^\circ - (90^\circ - x) = x$ olur.
- Şimdi $\triangle FDE$ ve $\triangle EBC$ üçgenlerini karşılaştıralım:
- $m(\angle D) = 90^\circ$ (kare olduğu için)
- $m(\angle C) = 90^\circ$ (kare olduğu için)
- $m(\angle DEF) = x$
- $m(\angle CBE) = x$
- Benzer üçgenlerde kenar oranları eşittir: $\frac{|DF|}{|EC|} = \frac{|DE|}{|CB|}$.
- Bilinen değerleri yerine yazalım: $\frac{|DF|}{4} = \frac{2}{6}$.
- Denklemi çözerek $|DF|$ uzunluğunu bulalım: $|DF| = \frac{2 \cdot 4}{6} = \frac{8}{6} = \frac{4}{3}$ birim.
- $\triangle FDE$ bir dik üçgendir ($m(\angle D) = 90^\circ$). $\tan x$ değerini bulmak için karşı dik kenarın komşu dik kenara oranını kullanırız.
- $\tan x = \frac{|DF|}{|DE|} = \frac{4/3}{2} = \frac{4}{3 \cdot 2} = \frac{4}{6} = \frac{2}{3}$.
- Doğru Seçenek B'dır.