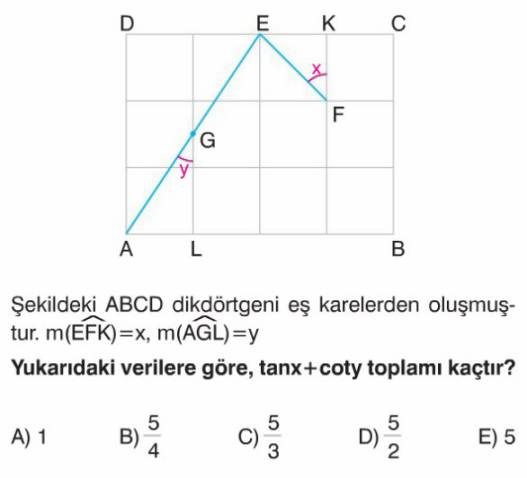
Soru Çözümü
- Bir karenin kenar uzunluğunu $1$ birim kabul edelim.
- Noktaların koordinatlarını belirleyelim: A$(0,0)$, L$(1,0)$, E$(2,3)$, K$(3,3)$, F$(3,2)$.
- $tanx$ değerini bulalım:
- $x = m(\widehat{EFK})$ açısı, F köşesindedir.
- E$(2,3)$, F$(3,2)$, K$(3,3)$ noktaları EFK dik üçgenini oluşturur. Dik açı K köşesindedir.
- Karşı kenar $EK = 3-2 = 1$ birimdir.
- Komşu kenar $FK = 3-2 = 1$ birimdir.
- $tanx = \frac{\text{Karşı Kenar}}{\text{Komşu Kenar}} = \frac{EK}{FK} = \frac{1}{1} = 1$.
- $coty$ değerini bulalım:
- $y = m(\widehat{AGL})$ açısı, G köşesindedir.
- G noktası, A$(0,0)$ ve E$(2,3)$ noktalarını birleştiren doğru üzerindedir ve $x=1$ düşey çizgisindedir.
- AE doğrusunun denklemi $Y = \frac{3}{2}X$'tir. $X=1$ için $Y = \frac{3}{2}$. Yani G$(1, \frac{3}{2})$.
- A$(0,0)$, L$(1,0)$, G$(1, \frac{3}{2})$ noktaları AGL dik üçgenini oluşturur. Dik açı L köşesindedir.
- Karşı kenar $AL = 1-0 = 1$ birimdir.
- Komşu kenar $GL = \frac{3}{2}-0 = \frac{3}{2}$ birimdir.
- $coty = \frac{\text{Komşu Kenar}}{\text{Karşı Kenar}} = \frac{GL}{AL} = \frac{3/2}{1} = \frac{3}{2}$.
- $tanx + coty$ toplamını hesaplayalım:
- $tanx + coty = 1 + \frac{3}{2} = \frac{2}{2} + \frac{3}{2} = \frac{5}{2}$.
- Doğru Seçenek D'dır.