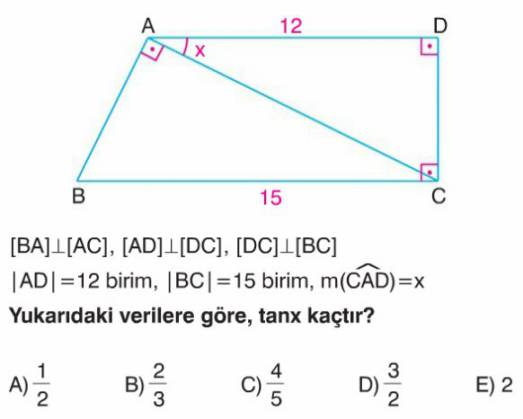
Soru Çözümü
- Verilen bilgilere göre, $\angle ADC = 90^\circ$ ve $\angle DCB = 90^\circ$ olduğundan, $AD \parallel BC$'dir. Bu durumda $ABCD$ bir dik yamuktur.
- A noktasından $BC$ kenarına bir dikme indirelim ve bu dikmenin ayağına $H$ diyelim. Bu durumda $ADCH$ bir dikdörtgen olur.
- Dikdörtgen özelliğinden dolayı $|HC| = |AD| = 12$ birim ve $|DC| = |AH|$ olur.
- $|BH|$ uzunluğunu bulalım: $|BH| = |BC| - |HC| = 15 - 12 = 3$ birim.
- $\triangle ABC$ bir dik üçgendir (çünkü $\angle BAC = 90^\circ$ verilmiştir). $AH$, $BC$ hipotenüsüne ait yüksekliktir.
- Öklid bağıntısına göre: $|AH|^2 = |BH| \cdot |HC|$. Buradan $|AH|^2 = 3 \cdot 12 = 36$ elde ederiz.
- $|AH| = \sqrt{36} = 6$ birimdir.
- $|DC| = |AH|$ olduğundan, $|DC| = 6$ birimdir.
- $\triangle ADC$ bir dik üçgendir (çünkü $\angle ADC = 90^\circ$). $tanx$ değerini hesaplayalım: $tanx = \frac{\text{karşı kenar}}{\text{komşu kenar}} = \frac{|DC|}{|AD|}$.
- $tanx = \frac{6}{12} = \frac{1}{2}$.
- Doğru Seçenek A'dır.