Soru Çözümü
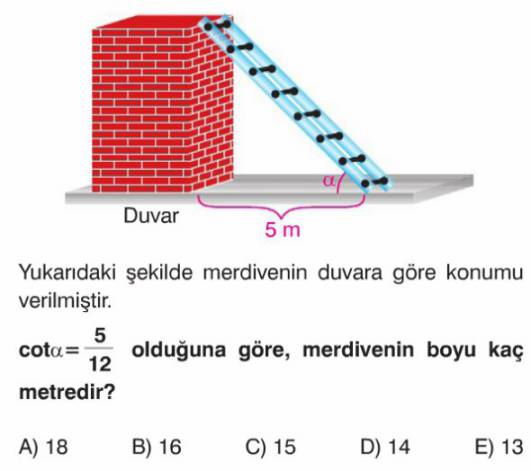
- Şekilde bir dik üçgen oluşmaktadır. Merdiven hipotenüs, duvarın yüksekliği ve yerdeki mesafe dik kenarlardır.
- $\alpha$ açısının komşu dik kenarı $5 m$'dir. Duvarın yüksekliğini $h$ olarak alalım.
- Kotanjant tanımına göre, $\cot\alpha = \frac{\text{komşu dik kenar}}{\text{karşı dik kenar}}$.
- Verilen $\cot\alpha = \frac{5}{12}$ ve şekilden $\cot\alpha = \frac{5}{h}$ eşitliğini yazabiliriz.
- Bu iki ifadeyi eşitleyerek duvarın yüksekliğini buluruz: $\frac{5}{h} = \frac{5}{12} \implies h = 12 m$.
- Merdivenin boyu $L$ olsun. Dik üçgende Pisagor Teoremi'ni uygularız: $L^2 = (\text{komşu dik kenar})^2 + (\text{karşı dik kenar})^2$.
- $L^2 = 5^2 + 12^2$.
- $L^2 = 25 + 144$.
- $L^2 = 169$.
- $L = \sqrt{169} = 13 m$.
- Doğru Seçenek E'dır.