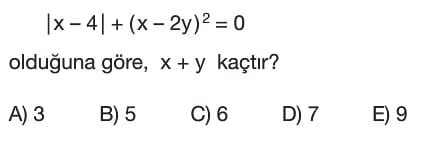
Soru Çözümü
- Verilen denklem $|x-4| + (x-2y)^2 = 0$'dır.
- Mutlak değer ve bir sayının karesi daima sıfıra eşit veya sıfırdan büyüktür. İki negatif olmayan ifadenin toplamının sıfır olması için her ikisinin de ayrı ayrı sıfır olması gerekir.
- Bu durumda, $|x-4| = 0$ ve $(x-2y)^2 = 0$ olmalıdır.
- İlk denklemden $x-4 = 0 \implies x = 4$ bulunur.
- İkinci denklemden $x-2y = 0$ bulunur.
- $x = 4$ değerini ikinci denkleme yerine koyarsak, $4-2y = 0 \implies 2y = 4 \implies y = 2$ olur.
- Bizden istenen $x+y$ değeridir. $x+y = 4+2 = 6$'dır.
- Doğru Seçenek C'dır.