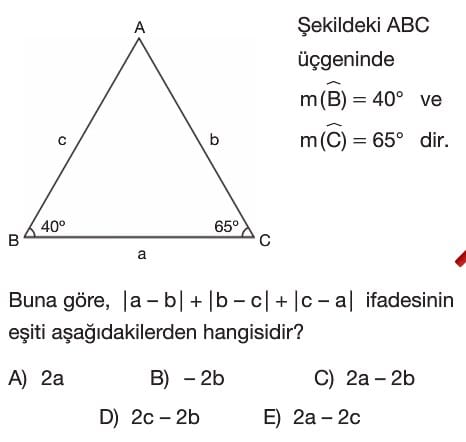
Soru Çözümü
- Üçgenin iç açıları toplamı $180^\circ$'dir. Verilen açılar $m(\hat{B}) = 40^\circ$ ve $m(\hat{C}) = 65^\circ$ olduğundan, $m(\hat{A}) = 180^\circ - (40^\circ + 65^\circ) = 180^\circ - 105^\circ = 75^\circ$ bulunur.
- Açıların büyüklük sıralaması $m(\hat{B}) < m(\hat{C}) < m(\hat{A})$ yani $40^\circ < 65^\circ < 75^\circ$'dir.
- Bir üçgende büyük açı karşısında büyük kenar bulunur. Bu nedenle kenar uzunlukları arasındaki sıralama $b < c < a$'dır.
- Mutlak değer ifadelerini açalım:
- $a > b$ olduğundan, $a - b > 0$. Dolayısıyla $|a - b| = a - b$.
- $b < c$ olduğundan, $b - c < 0$. Dolayısıyla $|b - c| = -(b - c) = c - b$.
- $c < a$ olduğundan, $c - a < 0$. Dolayısıyla $|c - a| = -(c - a) = a - c$.
- İfadeyi yerine koyup sadeleştirelim: $|a - b| + |b - c| + |c - a| = (a - b) + (c - b) + (a - c)$ $= a - b + c - b + a - c$ $= (a + a) + (-b - b) + (c - c)$ $= 2a - 2b + 0$ $= 2a - 2b$
- Doğru Seçenek C'dır.