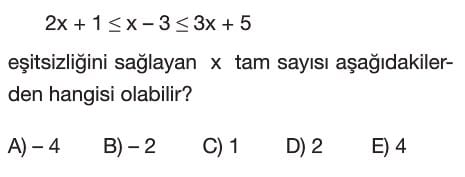
Soru Çözümü
- Verilen eşitsizlik $2x + 1 \leq x - 3 \leq 3x + 5$ iki parçaya ayrılır.
- Birinci Eşitsizlik: $2x + 1 \leq x - 3$
- $2x - x \leq -3 - 1$
- $x \leq -4$
- İkinci Eşitsizlik: $x - 3 \leq 3x + 5$
- $-3 - 5 \leq 3x - x$
- $-8 \leq 2x$
- Her iki tarafı $2$'ye böleriz: $\frac{-8}{2} \leq \frac{2x}{2}$
- $-4 \leq x$
- Her iki eşitsizliğin çözüm kümesi birleştirilir: $x \leq -4$ ve $x \geq -4$.
- Bu durum sadece $x = -4$ olduğunda sağlanır.
- Seçenekler arasında $x = -4$ tam sayısı A seçeneğinde bulunur.
- Doğru Seçenek A'dır.