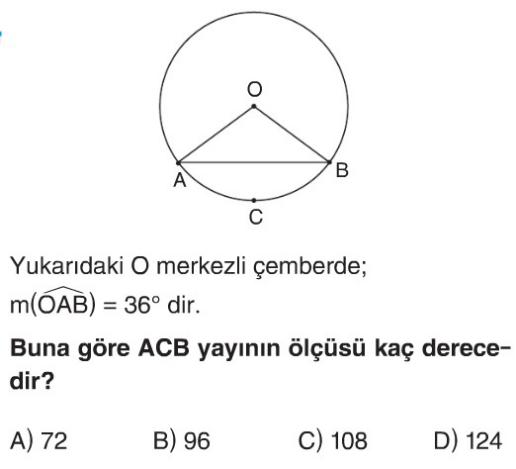
Soru Çözümü
- OA ve OB, O merkezli çemberin yarıçaplarıdır.
- Bu nedenle, OAB üçgeni bir ikizkenar üçgendir ($OA = OB$).
- İkizkenar üçgende taban açıları eşittir, yani $m(\widehat{OBA}) = m(\widehat{OAB})$.
- Soruda $m(\widehat{OAB}) = 36^\circ$ verildiği için $m(\widehat{OBA}) = 36^\circ$ olur.
- Bir üçgenin iç açıları toplamı $180^\circ$'dir. OAB üçgeninde merkez açı $m(\widehat{AOB})$'yi bulalım:
- $m(\widehat{AOB}) = 180^\circ - (m(\widehat{OAB}) + m(\widehat{OBA}))$
- $m(\widehat{AOB}) = 180^\circ - (36^\circ + 36^\circ) = 180^\circ - 72^\circ = 108^\circ$.
- Bir çemberde merkez açının ölçüsü, gördüğü yayın ölçüsüne eşittir.
- Bu durumda, AB yayının ölçüsü merkez açı $m(\widehat{AOB})$'ye eşit olup $108^\circ$'dir.
- Soruda "ACB yayı" ifadesi, seçenekler ve 7. sınıf seviyesi göz önüne alındığında, genellikle AB minor yayının veya merkez açı AOB'nin ölçüsünü ifade etmek için kullanılır.
- Dolayısıyla, ACB yayının ölçüsü $108^\circ$'dir.
- Doğru Seçenek C'dır.