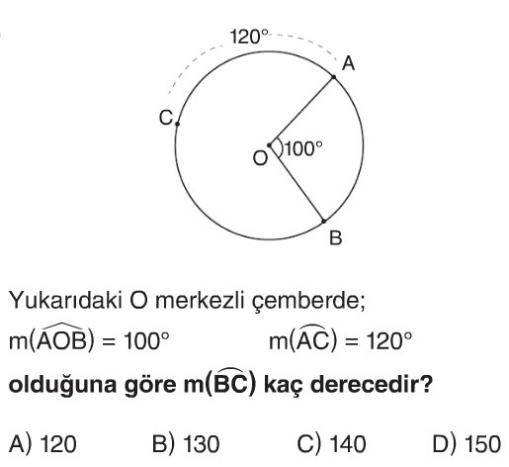
Soru Çözümü
- O merkezli çemberde, merkez açı $m(\text{AOB}) = 100^\circ$ verildiği için, bu açının gördüğü yay $m(\text{AB})$ de $100^\circ$'dir. Yani $m(\text{AB}) = 100^\circ$.
- Soruda $m(\text{AC}) = 120^\circ$ olarak verilmiştir.
- Bir çemberin çevresinin toplam ölçüsü $360^\circ$'dir. Bu durumda, yayların toplamı $m(\text{AB}) + m(\text{BC}) + m(\text{AC}) = 360^\circ$ olmalıdır.
- Verilen değerleri yerine koyarsak: $100^\circ + m(\text{BC}) + 120^\circ = 360^\circ$.
- Denklemi basitleştirirsek: $220^\circ + m(\text{BC}) = 360^\circ$.
- $m(\text{BC})$'yi bulmak için $360^\circ$'den $220^\circ$'yi çıkarırız: $m(\text{BC}) = 360^\circ - 220^\circ = 140^\circ$.
- Doğru Seçenek C'dır.