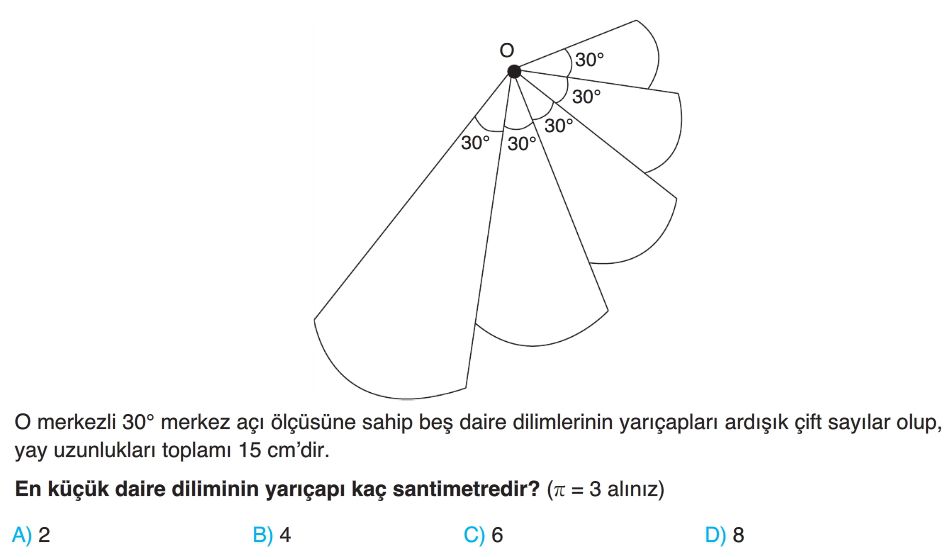
Soru Çözümü
- Bir daire diliminin yay uzunluğu formülü $L = 2 \pi r \frac{\alpha}{360^\circ}$ şeklindedir.
- Soruda verilen değerler $\alpha = 30^\circ$ ve $\pi = 3$'tür.
- Yay uzunluğu formülünde bu değerleri yerine yazarsak $L = 2 \cdot 3 \cdot r \cdot \frac{30^\circ}{360^\circ} = 6r \cdot \frac{1}{12} = \frac{r}{2}$ olur.
- Daire dilimlerinin yarıçapları ardışık çift sayılar olduğundan, en küçük yarıçap $r$ ise diğerleri $r+2$, $r+4$, $r+6$, $r+8$ olur.
- Bu yarıçaplara sahip daire dilimlerinin yay uzunlukları sırasıyla $\frac{r}{2}$, $\frac{r+2}{2}$, $\frac{r+4}{2}$, $\frac{r+6}{2}$, $\frac{r+8}{2}$'dir.
- Tüm yay uzunluklarının toplamı $15 cm$ olarak verilmiştir: $\frac{r}{2} + \frac{r+2}{2} + \frac{r+4}{2} + \frac{r+6}{2} + \frac{r+8}{2} = 15$
- Denklemi çözelim: $\frac{r + r+2 + r+4 + r+6 + r+8}{2} = 15$ $\frac{5r + 20}{2} = 15$ $5r + 20 = 30$ $5r = 10$ $r = 2$ cm
- Buna göre, en küçük daire diliminin yarıçapı $2 cm$'dir.
- Doğru Seçenek A'dır.