Soru Çözümü
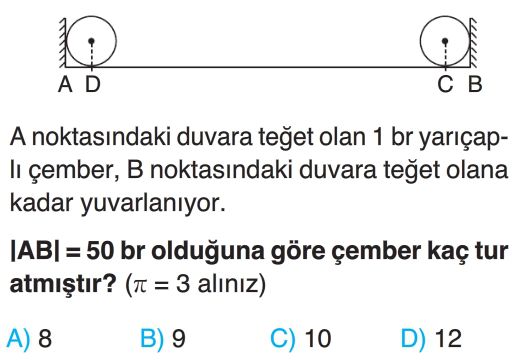
- Çemberin yarıçapı $r = 1$ br olarak verilmiştir.
- Çemberin duvarlar arasında hareket ettiği mesafe, merkezinin katettiği mesafedir. Çember, A duvarına teğet başladığı ve B duvarına teğet bittiği için, merkezi toplam $|AB|$ mesafesinden iki yarıçap kadar daha az yol alır.
- Merkezin katettiği mesafe: $|AB| - 2r = 50 - 2 \times 1 = 50 - 2 = 48$ br.
- Çemberin çevresi (bir turda katettiği mesafe) $C = 2 \pi r$ formülü ile bulunur.
- $\pi = 3$ ve $r = 1$ değerlerini yerine koyarsak, çemberin çevresi $C = 2 \times 3 \times 1 = 6$ br olur.
- Çemberin kaç tur attığını bulmak için, merkezin katettiği toplam mesafeyi çemberin çevresine böleriz. Tur sayısı = $48 / 6 = 8$.
- Doğru Seçenek A'dır.