Soru Çözümü
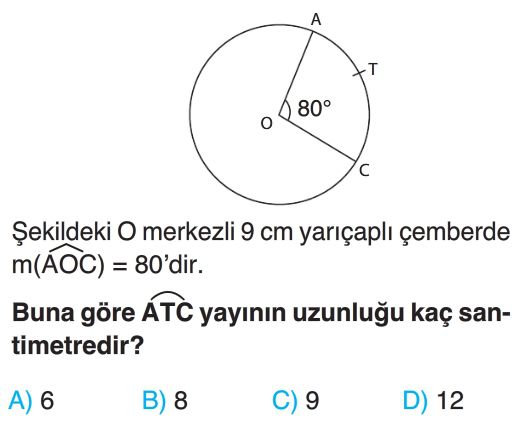
- Çemberin yarıçapı $r = 9 cm$ olarak verilmiştir.
- Merkez açı $m(\widehat{AOC}) = 80^\circ$ olarak verilmiştir. Bu açı, $\widehat{AC}$ yayını görür.
- 7. sınıf seviyesindeki sorularda genellikle $\pi$ değeri $3$ olarak alınır.
- Çemberin çevresi $C = 2\pi r$ formülüyle bulunur. Buna göre $C = 2 \times 3 \times 9 cm = 54 cm$.
- Bir yay uzunluğu, çevrenin merkez açıya karşılık gelen oranıyla bulunur: $L = C \times \frac{\text{merkez açı}}{360^\circ}$.
- $\widehat{AC}$ yayının uzunluğu $L(\widehat{AC}) = 54 cm \times \frac{80}{360}$ olarak hesaplanır.
- Sadeleştirme yapıldığında $\frac{80}{360} = \frac{8}{36} = \frac{2}{9}$ olur.
- Yay uzunluğu $L(\widehat{AC}) = 54 cm \times \frac{2}{9} = 6 \times 2 cm = 12 cm$ bulunur.
- Doğru Seçenek D'dır.