Soru Çözümü
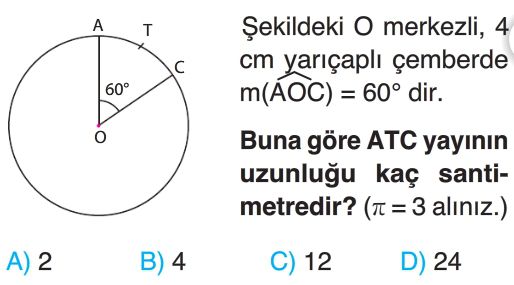
- Çemberin yarıçapı $r = 4 cm$ ve $\pi = 3$ olarak verilmiştir.
- Çemberin çevresi $C = 2 \pi r$ formülü ile hesaplanır.
- $C = 2 \cdot 3 \cdot 4 = 24 cm$
- $\widehat{AOC}$ merkez açısı $60^\circ$ olduğu için, $\widehat{AC}$ yayının uzunluğu, çemberin çevresinin $60^\circ / 360^\circ$ oranına eşittir.
- Yay uzunluğu $= (60^\circ / 360^\circ) \cdot 24 cm$
- Yay uzunluğu $= (1/6) \cdot 24 cm$
- Yay uzunluğu $= 4 cm$
- Doğru Seçenek B'dır.