Soru Çözümü
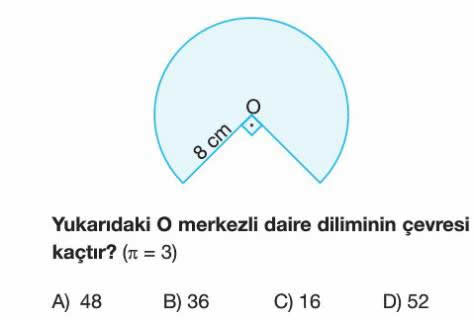
- Verilenler: Yarıçap $r = 8 cm$ ve $\pi = 3$.
- Şekildeki daire diliminin merkez açısı, gösterilen $90^\circ$ açının bütünleyeni olan $360^\circ - 90^\circ = 270^\circ$'dir.
- Tam dairenin çevresi $2\pi r$ formülüyle bulunur. Çevre $= 2 \times 3 \times 8 = 48 cm$.
- Daire diliminin yay uzunluğu, tam daire çevresinin merkez açının $360^\circ$'ye oranıyla bulunur. Yay uzunluğu $= 48 \times \frac{270}{360} = 48 \times \frac{3}{4} = 36 cm$.
- Daire diliminin çevresi, yay uzunluğu ile iki yarıçapın toplamıdır. Çevre $= 36 cm + 8 cm + 8 cm = 36 cm + 16 cm = 52 cm$.
- Doğru Seçenek D'dır.