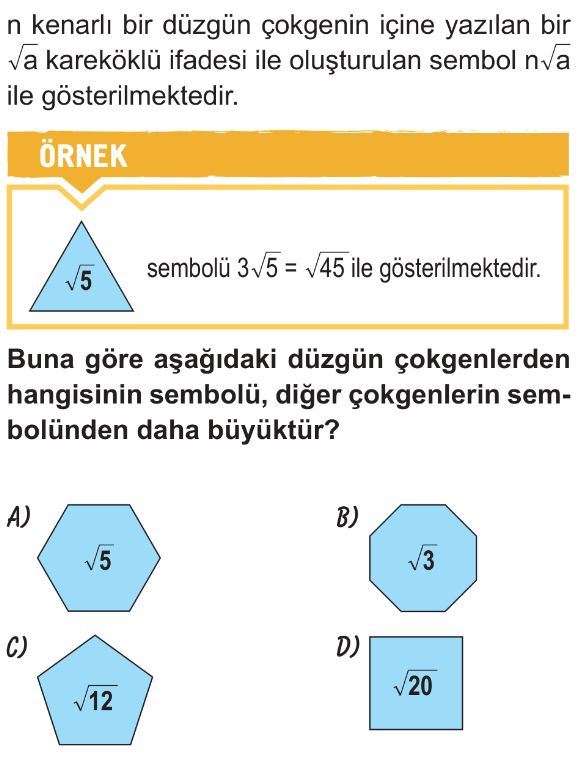
Soru Çözümü
- Sembol kuralı: n kenarlı düzgün çokgenin içine `$\sqrt{a}$` yazıldığında, sembol `$n\sqrt{a}$` olarak tanımlanır. Bu ifadeyi karşılaştırmak için `$\sqrt{n^2 a}$` şeklinde yazılır.
- A seçeneği (Altıgen): n=6, `$\sqrt{a} = \sqrt{5}$`. Sembol `$6\sqrt{5} = \sqrt{6^2 \times 5} = \sqrt{36 \times 5} = \sqrt{180}$`.
- B seçeneği (Sekizgen): n=8, `$\sqrt{a} = \sqrt{3}$`. Sembol `$8\sqrt{3} = \sqrt{8^2 \times 3} = \sqrt{64 \times 3} = \sqrt{192}$`.
- C seçeneği (Beşgen): n=5, `$\sqrt{a} = \sqrt{12}$`. Sembol `$5\sqrt{12} = \sqrt{5^2 \times 12} = \sqrt{25 \times 12} = \sqrt{300}$`.
- D seçeneği (Kare): n=4, `$\sqrt{a} = \sqrt{20}$`. Sembol `$4\sqrt{20} = \sqrt{4^2 \times 20} = \sqrt{16 \times 20} = \sqrt{320}$`.
- Karşılaştırma: Elde edilen değerler `$\sqrt{180}$`, `$\sqrt{192}$`, `$\sqrt{300}$` ve `$\sqrt{320}$`'dir. Bu değerler arasında en büyük olan `$\sqrt{320}$`'dir.
- Doğru Seçenek D'dır.