Soru Çözümü
- ABCD karesinin kenar uzunluğunu belirle.
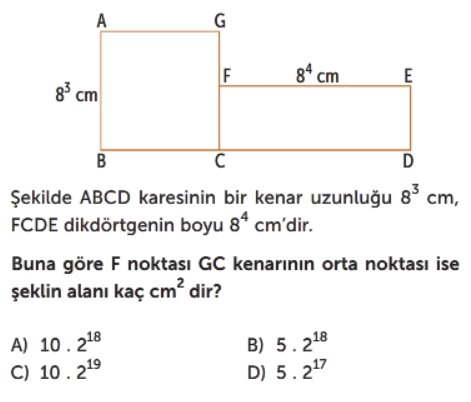
Verilen bilgiye göre, ABCD karesinin bir kenar uzunluğu $8^3$ cm'dir. Bu durumda $AB = BC = GC = 8^3$ cm olur. - F noktasının konumunu kullanarak FC uzunluğunu bul.
F noktası GC kenarının orta noktası olduğu için, $FC = \frac{GC}{2} = \frac{8^3}{2}$ cm'dir. - FCDE dikdörtgeninin kenar uzunluklarını belirle.
FCDE dikdörtgeninin boyu $8^4$ cm olarak verilmiştir, yani $CD = FE = 8^4$ cm'dir. Dikdörtgenin eni ise $FC = \frac{8^3}{2}$ cm'dir. - ABCD karesinin alanını hesapla.
Karenin alanı $A_{ABCD} = (8^3)^2 = 8^6$. Tabanı $2^3$ olarak yazarsak, $A_{ABCD} = (2^3)^6 = 2^{18}$ cm$^2$. - FCDE dikdörtgeninin alanını hesapla.
Dikdörtgenin alanı $A_{FCDE} = \text{boy} \times \text{en} = 8^4 \times \frac{8^3}{2} = \frac{8^{4+3}}{2} = \frac{8^7}{2}$. Tabanı $2^3$ olarak yazarsak, $A_{FCDE} = \frac{(2^3)^7}{2} = \frac{2^{21}}{2^1} = 2^{21-1} = 2^{20}$ cm$^2$. - Şeklin toplam alanını bul.
Toplam alan $A_{toplam} = A_{ABCD} + A_{FCDE} = 2^{18} + 2^{20}$. $2^{20}$ ifadesini $2^{18}$ cinsinden yazarsak, $2^{20} = 2^2 \cdot 2^{18} = 4 \cdot 2^{18}$. Böylece, $A_{toplam} = 2^{18} + 4 \cdot 2^{18} = (1+4) \cdot 2^{18} = 5 \cdot 2^{18}$ cm$^2$. - Doğru Seçenek B'dır.