Soru Çözümü
- Verilen üslü ifadelerin çarpımını bulalım: $x^3 \cdot x^2 \cdot x^8 \cdot x^{-5} \cdot x^{-4} \cdot x^{-3} = x^{(3+2+8-5-4-3)} = x^1 = x$. Bu, tabloda yeşil boyalı 6 hücreye yazılacak tüm sayıların çarpımıdır.
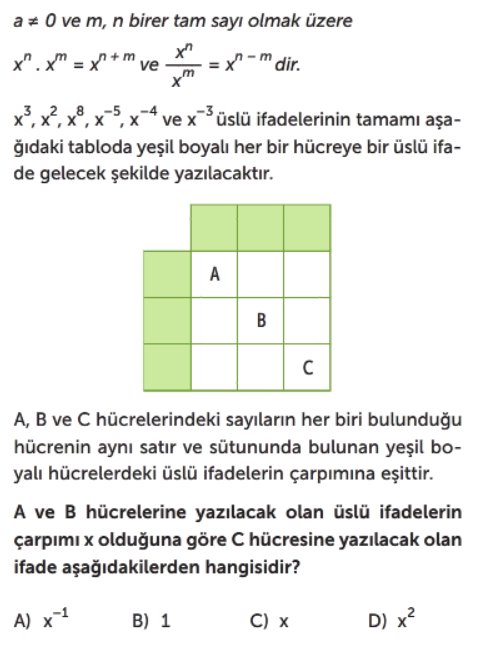
- Tablodaki yeşil hücreleri konumlarına göre adlandıralım: $G_{11}, G_{12}, G_{13}$ (1. satır), $G_{21}$ (2. satır, 1. sütun), $G_{31}$ (3. satır, 1. sütun), $G_{41}$ (4. satır, 1. sütun).
- A, B ve C hücrelerindeki değerleri tanımlayalım:
- $A = G_{21} \cdot G_{12}$ (A, 2. satır ve 2. sütundaki yeşil hücrelerin çarpımıdır)
- $B = G_{31} \cdot G_{12}$ (B, 3. satır ve 2. sütundaki yeşil hücrelerin çarpımıdır)
- $C = G_{31} \cdot G_{13}$ (C, 3. satır ve 3. sütundaki yeşil hücrelerin çarpımıdır)
- Soruda $A \cdot B = x$ olduğu verilmiştir. A ve B'nin tanımlarını yerine yazalım: $(G_{21} \cdot G_{12}) \cdot (G_{31} \cdot G_{12}) = x$ $G_{21} \cdot G_{31} \cdot (G_{12})^2 = x$.
- Tüm yeşil hücrelerin çarpımı $P_{tüm} = G_{11} \cdot G_{12} \cdot G_{13} \cdot G_{21} \cdot G_{31} \cdot G_{41} = x$'tir.
- $P_{tüm}$ ile $A \cdot B$ değerlerini birbirine eşitleyelim, çünkü ikisi de $x$'e eşittir: $G_{11} \cdot G_{12} \cdot G_{13} \cdot G_{21} \cdot G_{31} \cdot G_{41} = G_{21} \cdot G_{31} \cdot (G_{12})^2$. Eşitliğin her iki tarafını $G_{21} \cdot G_{31} \cdot G_{12}$ ile bölelim (üssü ifadeler sıfır olamaz): $G_{11} \cdot G_{13} \cdot G_{41} = G_{12}$.
- C hücresindeki ifadeyi bulmamız isteniyor: $C = G_{31} \cdot G_{13}$.
- Verilen üslü ifadeler kümesi $\{x^3, x^2, x^8, x^{-5}, x^{-4}, x^{-3}\}$'tür. C'nin tek bir değeri olması için, $G_{31}$ ve $G_{13}$'ün çarpımının sabit bir değer olması gerekir. Bu, $G_{31}$ ve $G_{13}$'ün birbirinin çarpmaya göre tersi olması durumunda gerçekleşir. Verilen listede tek ters çifti $x^3$ ve $x^{-3}$'tür.
- Bu durumda, $G_{31}$ ve $G_{13}$ hücrelerine $x^3$ ve $x^{-3}$ ifadeleri yerleştirilmelidir (sırası önemli değildir). Bu durumda $C = x^3 \cdot x^{-3} = x^{(3-3)} = x^0 = 1$.
- Bu atamanın diğer koşullarla tutarlı olduğunu kontrol edelim:
- $G_{31} = x^3$ ve $G_{13} = x^{-3}$ olsun. (C=1)
- Kalan ifadeler: $\{x^2, x^8, x^{-5}, x^{-4}\}$. Bunlar $G_{11}, G_{12}, G_{21}, G_{41}$ hücrelerine atanacaktır.
- $A \cdot B = G_{21} \cdot G_{31} \cdot (G_{12})^2 = x$ koşulunu kullanalım: $G_{21} \cdot x^3 \cdot (G_{12})^2 = x$. Bu da $G_{21} \cdot (G_{12})^2 = x^{-2}$ demektir.
- Kalan ifadelerden $G_{12} = x^{-5}$ ve $G_{21} = x^8$ seçersek: $x^8 \cdot (x^{-5})^2 = x^8 \cdot x^{-10} = x^{-2}$. Bu koşul sağlanır.
- Kalan ifadeler $G_{11}$ ve $G_{41}$ için $\{x^2, x^{-4}\}$ olur.
- Daha önce bulduğumuz $G_{11} \cdot G_{13} \cdot G_{41} = G_{12}$ ilişkisini kontrol edelim: $x^2 \cdot x^{-3} \cdot x^{-4} = x^{(2-3-4)} = x^{-5}$. Bu da $G_{12}$'ye eşittir ($x^{-5}$). Tüm koşullar sağlanır.
- Bu nedenle, C hücresine yazılacak ifade 1'dir.
- Doğru Seçenek B'dır.