Soru Çözümü
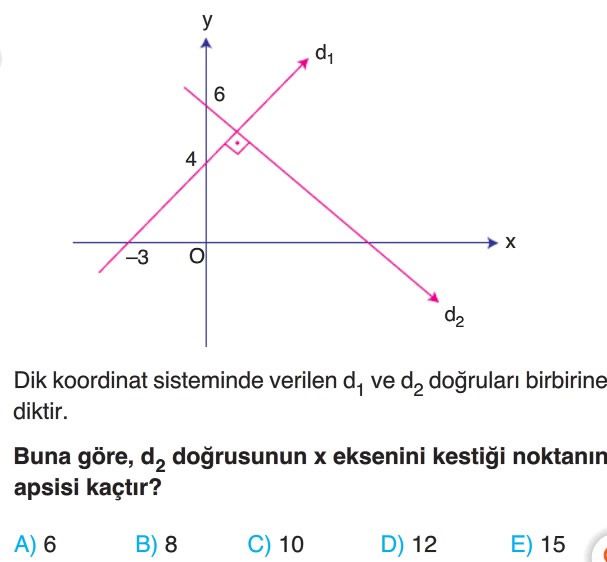
- $d_1$ doğrusunun geçtiği noktalar $(-3, 0)$ ve $(0, 4)$'tür.
- $d_1$ doğrusunun eğimi $m_1 = \frac{4 - 0}{0 - (-3)} = \frac{4}{3}$'tür.
- $d_1$ ve $d_2$ doğruları birbirine dik olduğundan eğimleri çarpımı $-1$'dir. Yani $m_1 \cdot m_2 = -1$.
- $m_2 = \frac{-1}{m_1} = \frac{-1}{4/3} = -\frac{3}{4}$'tür.
- $d_2$ doğrusu $(0, 6)$ noktasından geçmektedir ve eğimi $m_2 = -\frac{3}{4}$'tür.
- $d_2$ doğrusunun denklemi $y - 6 = -\frac{3}{4}(x - 0)$ şeklinde yazılır.
- Denklemi düzenlersek $4(y - 6) = -3x \Rightarrow 4y - 24 = -3x \Rightarrow 3x + 4y - 24 = 0$ elde edilir.
- $d_2$ doğrusunun x eksenini kestiği noktayı bulmak için $y = 0$ yazılır.
- $3x + 4(0) - 24 = 0 \Rightarrow 3x - 24 = 0 \Rightarrow 3x = 24 \Rightarrow x = 8$'dir.
- Doğru Seçenek B'dır.