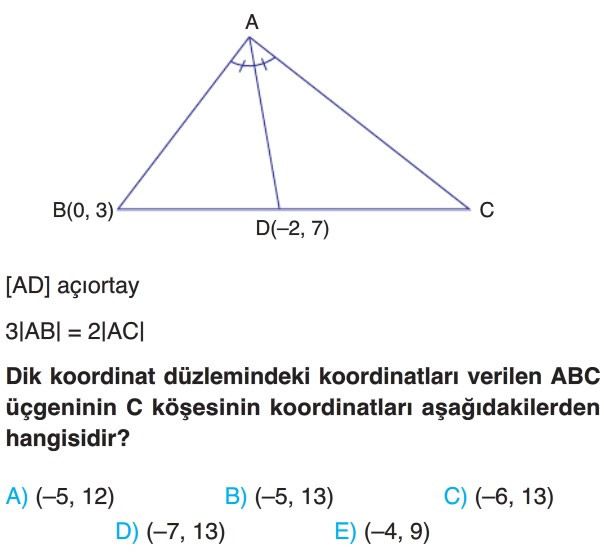
Soru Çözümü
- Verilen $3|AB| = 2|AC|$ eşitliğinden, $\frac{|AB|}{|AC|} = \frac{2}{3}$ oranı elde edilir.
- ABC üçgeninde [AD] açıortay olduğundan, Açıortay Teoremi'ne göre $\frac{|AB|}{|AC|} = \frac{|BD|}{|DC|}$ olur.
- Bu durumda, $\frac{|BD|}{|DC|} = \frac{2}{3}$'tür. Yani D noktası, BC doğru parçasını B'den itibaren $2:3$ oranında böler.
- C noktasının koordinatları $(x_C, y_C)$ olsun. B noktasının koordinatları $(0, 3)$ ve D noktasının koordinatları $(-2, 7)$'dir.
- D noktasının x koordinatı için formülü uygulayalım: $x_D = \frac{3 \cdot x_B + 2 \cdot x_C}{2+3}$ yani $-2 = \frac{3 \cdot 0 + 2 \cdot x_C}{5}$.
- Bu denklemi çözerek $2x_C = -10$, dolayısıyla $x_C = -5$ bulunur.
- D noktasının y koordinatı için formülü uygulayalım: $y_D = \frac{3 \cdot y_B + 2 \cdot y_C}{2+3}$ yani $7 = \frac{3 \cdot 3 + 2 \cdot y_C}{5}$.
- Bu denklemi çözerek $35 = 9 + 2y_C$, dolayısıyla $2y_C = 26$ ve $y_C = 13$ bulunur.
- C köşesinin koordinatları $(-5, 13)$'tür.
- Doğru Seçenek B'dır.