Soru Çözümü
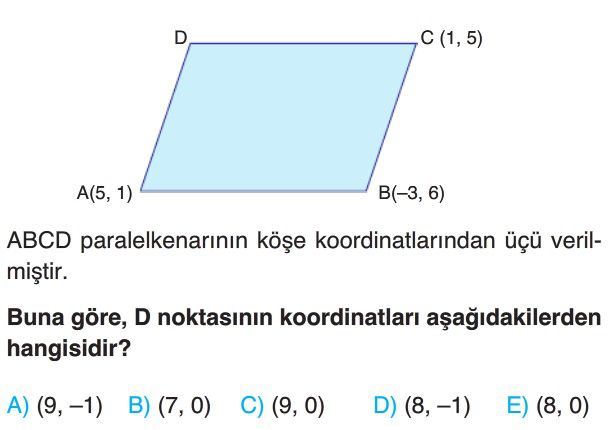
- Bir paralelkenarda köşegenler birbirini ortalar. Bu nedenle, AC köşegeninin orta noktası ile BD köşegeninin orta noktası aynıdır.
- Verilen noktalar $A(5, 1)$, $B(-3, 6)$ ve $C(1, 5)$'tir. D noktasının koordinatları $D(x, y)$ olsun.
- AC köşegeninin orta noktasının x-koordinatı: $\frac{x_A + x_C}{2} = \frac{5 + 1}{2} = \frac{6}{2} = 3$.
- BD köşegeninin orta noktasının x-koordinatı: $\frac{x_B + x_D}{2} = \frac{-3 + x}{2}$.
- Bu iki x-koordinatını eşitleyelim: $\frac{-3 + x}{2} = 3 \Rightarrow -3 + x = 6 \Rightarrow x = 9$.
- AC köşegeninin orta noktasının y-koordinatı: $\frac{y_A + y_C}{2} = \frac{1 + 5}{2} = \frac{6}{2} = 3$.
- BD köşegeninin orta noktasının y-koordinatı: $\frac{y_B + y_D}{2} = \frac{6 + y}{2}$.
- Bu iki y-koordinatını eşitleyelim: $\frac{6 + y}{2} = 3 \Rightarrow 6 + y = 6 \Rightarrow y = 0$.
- Buna göre, D noktasının koordinatları $D(9, 0)$ olarak bulunur.
- Doğru Seçenek C'dır.