Soru Çözümü
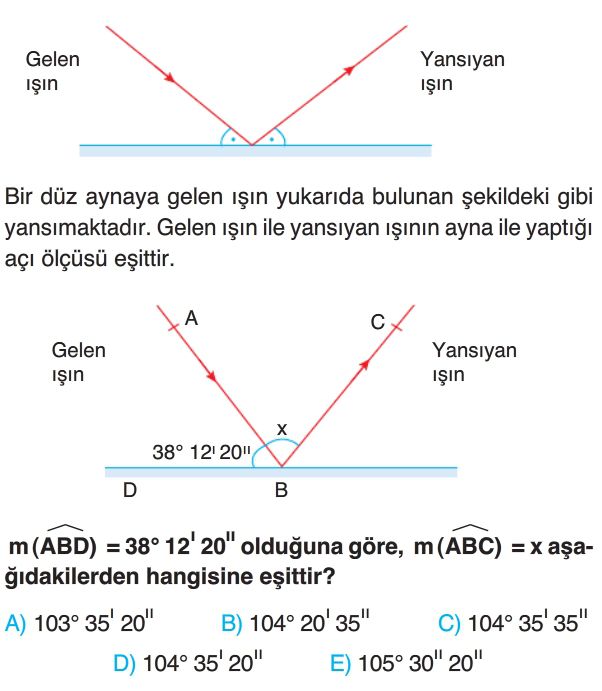
- Soruda verilen bilgiye göre, gelen ışın ile yansıyan ışının ayna ile yaptığı açı ölçüleri eşittir. Bu durumda, $m(\widehat{ABD}) = m(\widehat{CBD})$ olur.
- $m(\widehat{ABD}) = 38^\circ 12' 20''$ olarak verildiğinden, $m(\widehat{CBD}) = 38^\circ 12' 20''$ olur.
- Düz ayna üzerindeki B noktasında oluşan $\widehat{ABD}$, $\widehat{ABC}$ ($x$) ve $\widehat{CBD}$ açıları bir doğru açı oluşturur. Dolayısıyla bu açıların toplamı $180^\circ$'dir.
- Denklemi kuralım: $m(\widehat{ABD}) + m(\widehat{ABC}) + m(\widehat{CBD}) = 180^\circ$.
- Değerleri yerine yazalım: $38^\circ 12' 20'' + x + 38^\circ 12' 20'' = 180^\circ$.
- Açıları toplayalım: $38^\circ 12' 20'' + 38^\circ 12' 20'' = 76^\circ 24' 40''$.
- Denklem $x + 76^\circ 24' 40'' = 180^\circ$ haline gelir.
- $x$ değerini bulmak için çıkarma işlemi yapalım: $x = 180^\circ - 76^\circ 24' 40''$.
- $180^\circ$'yi $179^\circ 59' 60''$ olarak yazabiliriz.
- $x = 179^\circ 59' 60'' - 76^\circ 24' 40'' = 103^\circ 35' 20''$.
- Doğru Seçenek A'dır.