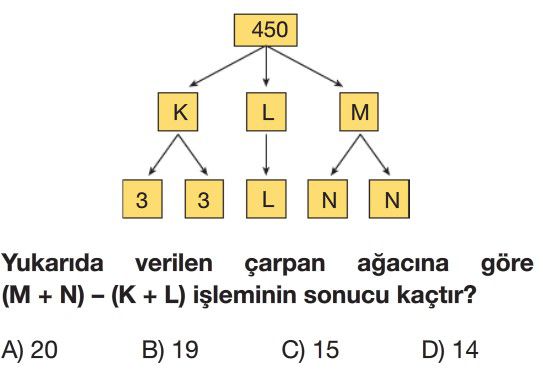
Soru Çözümü
- K değerini bulma: Çarpan ağacına göre K, 3 ve 3'ün çarpımıdır. Bu durumda $K = 3 \times 3 = 9$.
- 450'nin asal çarpanlarını bulma: 450 sayısının asal çarpanları $450 = 2 \times 3^2 \times 5^2$ şeklindedir. Yani asal çarpanlar 2, 3, 3, 5, 5'tir.
- L ve N değerlerini bulma: Çarpan ağacının en altındaki sayılar 3, 3, L, N, N'dir ve bunlar 450'nin asal çarpanlarıdır. İki tane 3 zaten ağaçta mevcut. Geriye kalan asal çarpanlar 2, 5, 5 olmalıdır. N iki kez tekrarlandığı için $N = 5$ olmalıdır. Bu durumda $L = 2$ olur.
- M değerini bulma: Çarpan ağacına göre M, N ve N'nin çarpımıdır. $N = 5$ olduğundan $M = 5 \times 5 = 25$.
- İfadeyi hesaplama: İstenen ifade $(M + N) - (K + L)$ şeklindedir.
- $M + N = 25 + 5 = 30$
- $K + L = 9 + 2 = 11$
- $(M + N) - (K + L) = 30 - 11 = 19$
- Doğru Seçenek B'dır.