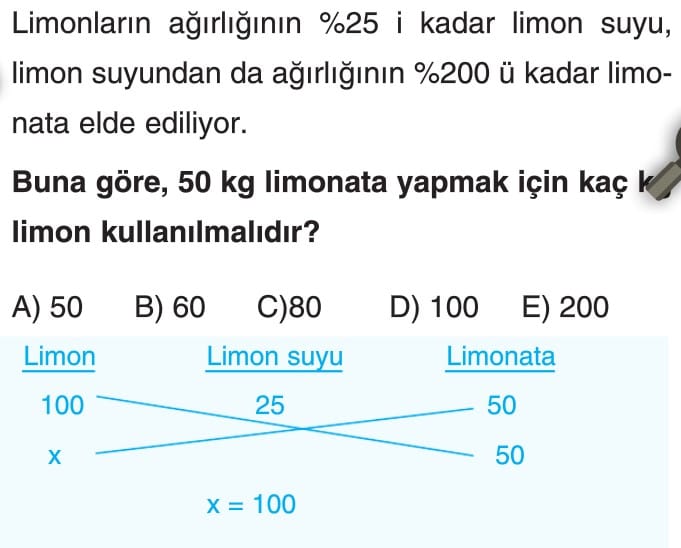
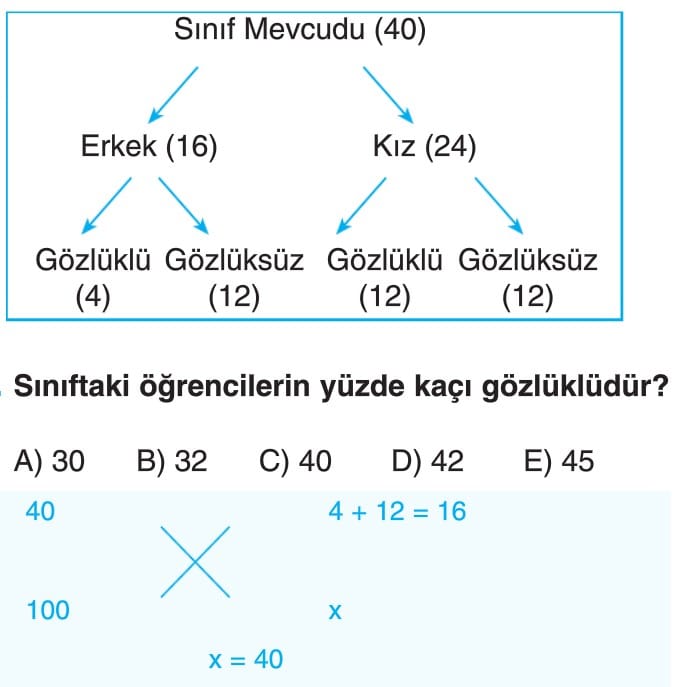
Yüzde Problemleri Soru Çözümleri

Yüzde Nedir: Paydası 100 ile ifade edilen bir oran yüzde olarak adlandırılır. 25/100 kesri 0,25 veya yüzde 25 demektir. % a ifadesi yüzde a olarak okunur ve % a = a/100 dür. Bir x sayısının % a sı x. a/100 = x.a/100 dür.
Bilgi: Yüzde problemlerini çözerken problemin durumuna göre, ifadenin tamamı 100x veya 100 alınabilir. Bu durum problemin çözümünde kolaylık sağlar.

Örnek: Bir ilimizde ilköğretim okullarının tüm okullar içindeki payı 2010 yılında % 5, 2015 yılında ise % 17,5 tur. Bu ilde 2010 – 2015 yılları arasında açılan 100 okulun 30 u ilköğretim okuludur. Buna göre, bu ilde 2010 yılında kaç ilköğretim okulu vardır?

Örnek: Bir sınıftaki öğrencilerin % 80 i matematik dersinden yıl sonunda geçmiş, bütünlemeye kalanların ise % 15 i bu dersten geçmiştir. Buna göre, sınıfın yüzde kaçı matematik dersinden geçmiştir?

Çözüm: Sınıftaki öğrenci sayısı 100 olsun. 100 öğrencinin % 80 i yani 80 öğrenci yıl sonu matematikten geçmiştir. 100 – 80 = 20 öğrenci bütünlemeye kalmıştır. 20 öğrencinin % 15 i olan 3 öğrenci bütünlemede geçmiştir. Buna göre, 100 öğrencinin 80 + 3 = 83 ü, diğer bir ifadeyle % 83 ü matematik dersinden geçmiştir.

Örnek: Can matematik dersinin 1. sınavında 75 almıştır. 2. sınav notu 1. sınava göre % 20 azalmış, 3. sınav notu ise 2. sınav notuna göre % 50 artmıştır. Buna göre, Can’ın 3. sınav notu kaçtır?
Çözüm: 2. sınav notu 1. sınava göre % 20 azalmış ise, 2. sınav notu 1. sınav notunun % 20 eksiğidir. Buradan, 2. sınav notu 75-75.20/100=75-15=60 olur. 3. sınav notu ise 2. sınav notuna göre % 50 artmış ise, 3. sınav notu 2. sınav notunun % 50 fazlasıdır. Buradan, 3. sınav notu 60+60.50/100=60+30=90 olur.

• Yüzde problemleri çözerken dikkat edilmesi gereken noktalar:
• Problemde verilen miktarın cinsi ve birimi dikkate alınmalıdır.
• Problemde verilen yüzdenin neyi ifade ettiği dikkate alınmalıdır.
• Kar-zarar problemlerinde, satılan fiyatın alımında ödenen fiyattan fazla olması durumunda kar, az olması durumunda ise zarar söz konusu olduğu unutulmamalıdır.
• Karışım problemlerinde, karıştırılan miktarların oranları ve nitelikleri dikkate alınmalıdır.

Çözümlü Örnek Test Soruları

Soru 1:
Bir ürünün fiyatı %20 artırıldığında 120 TL oluyor. Ürünün ilk fiyatı kaç TL’dir?

A) 90
B) 95
C) 100
D) 105
E) 110

Çözüm:
120 TL, fiyatın %120’si olduğuna göre, ilk fiyatı bulmak için 120 / 1.2 işlemi yapılır. İlk fiyat 100 TL’dir.
Doğru cevap: C) 100

Soru 2:
Bir miktarın %15’i 45 TL ise, bu miktar kaç TL’dir?

A) 200
B) 250
C) 300
D) 350
E) 400

Çözüm:
%15’i 45 TL olduğuna göre, miktarı bulmak için 45 / 0.15 işlemi yapılır. Miktar 300 TL’dir.
Doğru cevap: C) 300

Soru 3:
Bir arabanın fiyatı %25 indirimle 30.000 TL oldu. İndirimden önceki fiyatı kaç TL idi?

A) 35.000
B) 37.500
C) 40.000
D) 42.500
E) 45.000

Çözüm:
30.000 TL, fiyatın %75’ine denk gelir. İndirimden önceki fiyatı bulmak için 30.000 / 0.75 işlemi yapılır.
Doğru cevap: C) 40.000

Soru 4:
Bir ürüne %30 zam yapılırsa fiyatı 78 TL oluyor. Bu ürünün zamdan önceki fiyatı nedir?

A) 50
B) 55
C) 60
D) 65
E) 70

Çözüm:
%130’si 78 TL olduğuna göre, zamdan önceki fiyatı bulmak için 78 / 1.3 işlemi yapılır.
Doğru cevap: C) 60

Soru 5:
Bir okuldaki öğrencilerin %40’ı erkek, %60’ı kızdır. Erkek öğrencilerin sayısı 120 ise, okulda toplam kaç öğrenci vardır?

A) 150
B) 200
C) 250
D) 300
E) 350

Çözüm:
Erkek öğrenciler toplamın %40’ına denk geliyor. Toplam öğrenci sayısını bulmak için 120 / 0.4 işlemi yapılır.
Doğru cevap: D) 300

Soru 6:
Bir mağaza satışlarını %40 artırarak aylık satış miktarını 210.000 TL’ye çıkardı. Artıştan önce mağazanın satış miktarı ne kadardı?

A) 120.000
B) 130.000
C) 140.000
D) 150.000
E) 160.000

Çözüm:
Artıştan önceki satış miktarını bulmak için 210.000 / 1.4 işlemi yapılır.
Doğru cevap: E) 150.000

Soru 7:
Bir miktarın %80’i 160 TL ise, bu miktarın %25’i kaç TL’dir?

A) 40
B) 50
C) 60
D) 80
E) 100

Çözüm:
Önce toplam miktarı bulmak için 160 / 0.8 işlemi yapılır (200 TL). Sonra %25’i hesaplanır: 200 x 0.25 = 50 TL
Doğru cevap: B) 50

Soru 8:
Bir ürünün fiyatı %30 azaltıldığında 280 TL oluyor. İndirimden önceki fiyatı kaç TL idi?

A) 320
B) 350
C) 370
D) 400
E) 450

Çözüm:
280 TL, fiyatın %70’ine denk gelir. İndirimden önceki fiyatı bulmak için 280 / 0.7 işlemi yapılır.
Doğru cevap: D) 400