Yansıma 8. Sınıf
Bir şeklin bir doğruya göre simetrisi alınırsa elde edilen şekil, ilk şeklin doğruya göre yansımasıdır. Yansımada şeklin boyutu ve biçimi değişmez, yeri ve yönü değişir. Doğruya göre simetride şekil ile yansıması eştir.

Dikkat: Yansıma, doğru simetrisi ve ayna simetrisi kavramları aynı şeyi ifade eder.
ı. NOKTA, DOĞRU PARÇASI VE DİĞER ŞEKİLLERİN DÜZLEMDE YANSIMALARI
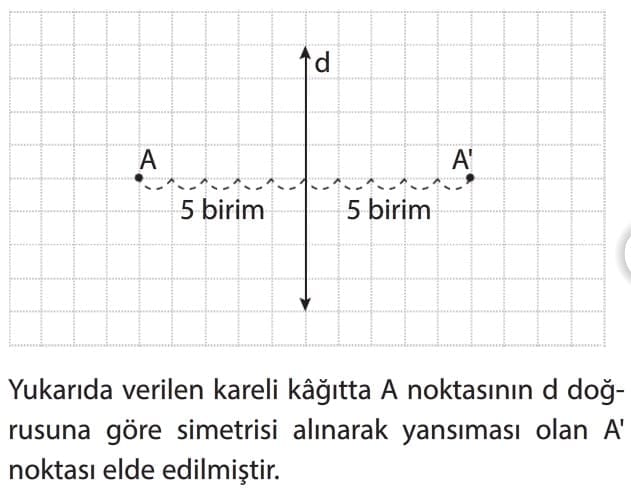
Dikkat: Doğruya göre simetride nokta ile yansımasının doğruya uzaklıkları eşittir.
Önemli Bilgi: Bir doğru parçasının yansıması bulunurken doğru parçasının uç noktalarının yansıması alınır. Daha sonra elde edilen noktalar birleştirilerek doğru parçasının yansıması bulunur.
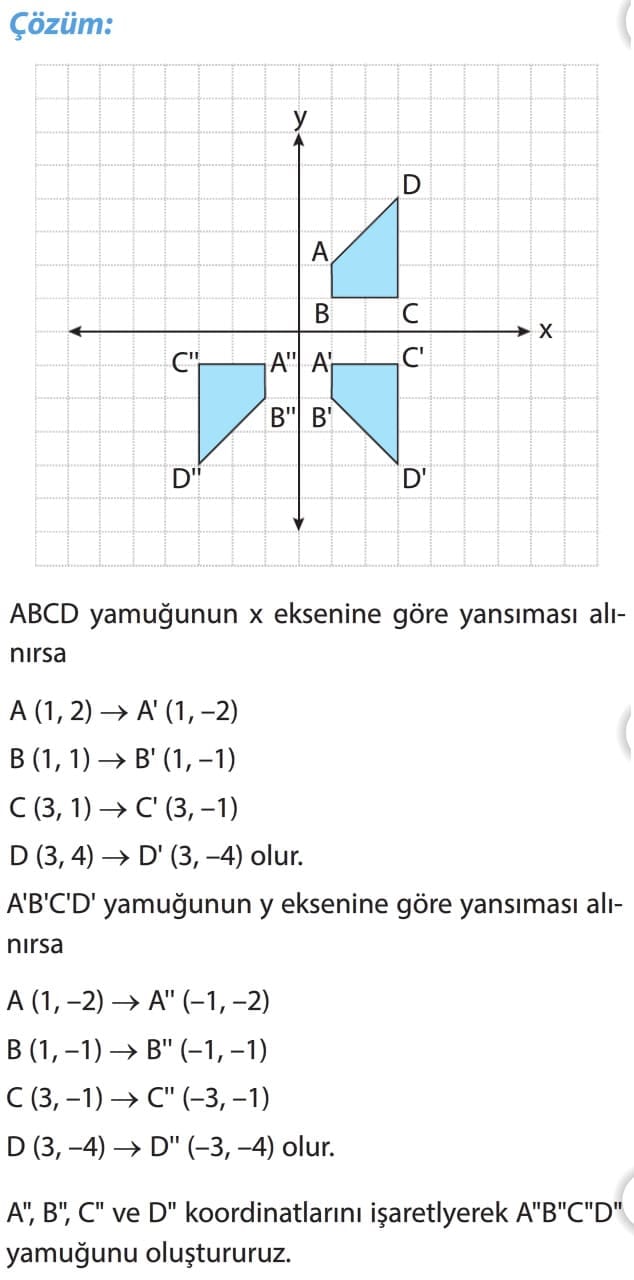
Önemli Bilgi: Bir şeklin yansıması bulunurken köşe noktalarının yansıması alınarak elde edilen noktalar birleştirilir.
Önemli Bilgi: Yansımada şekil ile görüntüsü üzerinde birbirine karşılık gelen noktalar simetri doğrusuna göre diktir.
2. NOKTA, DOĞRU PARÇASI VE DİĞER ŞEKİLLERİN KOORDİNAT DÜZLEMİNDE YANSIMALARI
Dikkat: Bir noktanın koordinatının önündeki “-” sembolü yansımada koordinatın işaret değiştirmesini ifade eder.
Önemli Bilgi: Koordinat düzleminde nokta, doğru parçası ve diğer şekillerin eksenlere göre birer defa arka arkaya yapılan yansıması orijine göre yansımayı verir. Yani hem X hem de y eksenine göre aynı anda yapılan yansımadır.
A (x, y) →A’ (-x, -y)
Orijine göre yansımada noktanın apsisi ve ordinatı işaret değiştirir.
Yansıma 8. Sınıf konu anlatımı Lgs Çözümlü Sorular
Örnek Soru: Yukarıda verilen kareli kâğıttaki K noktasının m doğrusuna göre yansıması K' noktasıdır. Buna göre, Kve K' noktaları arasındaki en kısa uzaklığı bulalım.
Çözüm: Nokta ile yansıması doğruya eşit uzaklıkta olduğundan K ile K' noktaları arasında uzaklık 3 + 3 = 6 birim olur.
Örnek Soru: Yukarıda kareli kâğıtta verilen AB doğru parçasının d doğrusuna göre yansımasını bulalım.
Çözüm: AB doğru parçasının yansımasını bulmak için A noktasını yansıtarak A' noktasını, B noktasını yansıtarak B' noktasını elde ettikten sonra bu noktaları birleştiriniz.
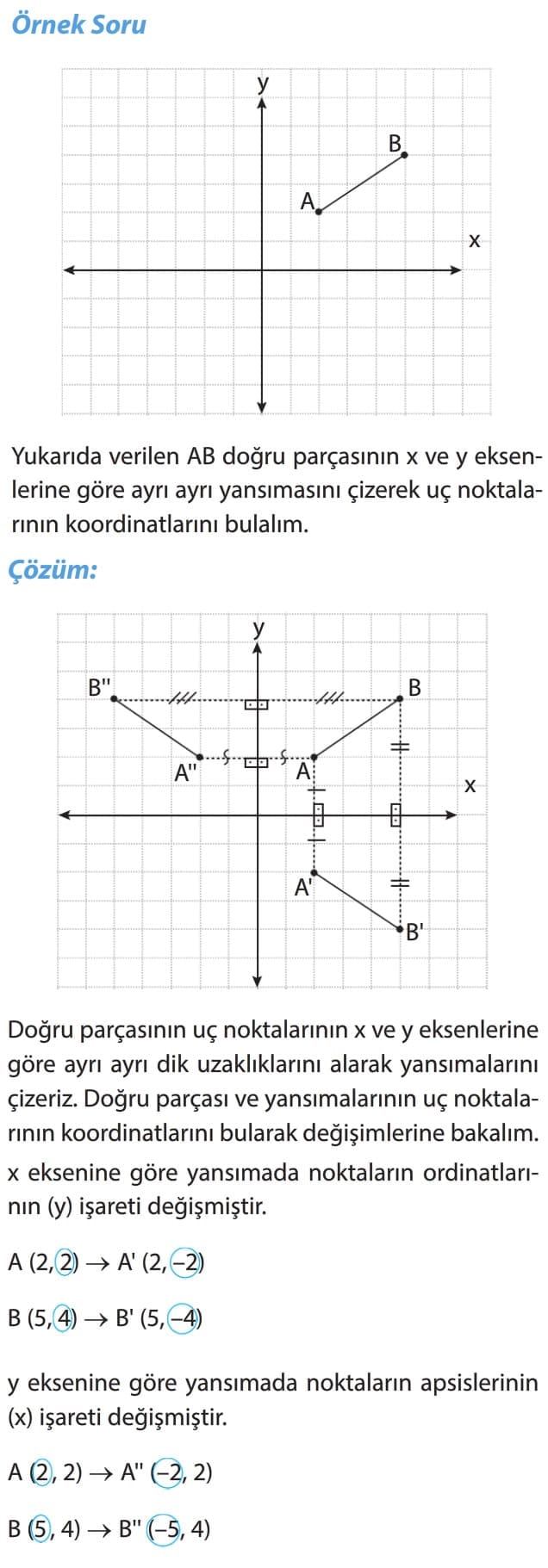
Örnek Soru: Yukarıda verilen AB doğru parçasının x ve y eksenlerine göre ayrı ayrı yansımasını çizerek uç noktalarının koordinatlarını bulalım.
Çözüm: Doğru parçasının uç noktalarının x ve y eksenlerine göre ayrı ayrı dik uzaklıklarını alarak yansımalarını çizeriz. Doğru parçası ve yansımalarının uç noktalarının koordinatlarını bularak değişimlerine bakalım. x eksenine göre yansımada noktaların ordinatlarının (y) işareti değişmiştir. y eksenine göre yansımada noktaların apsislerinin (x) işareti değişmiştir.
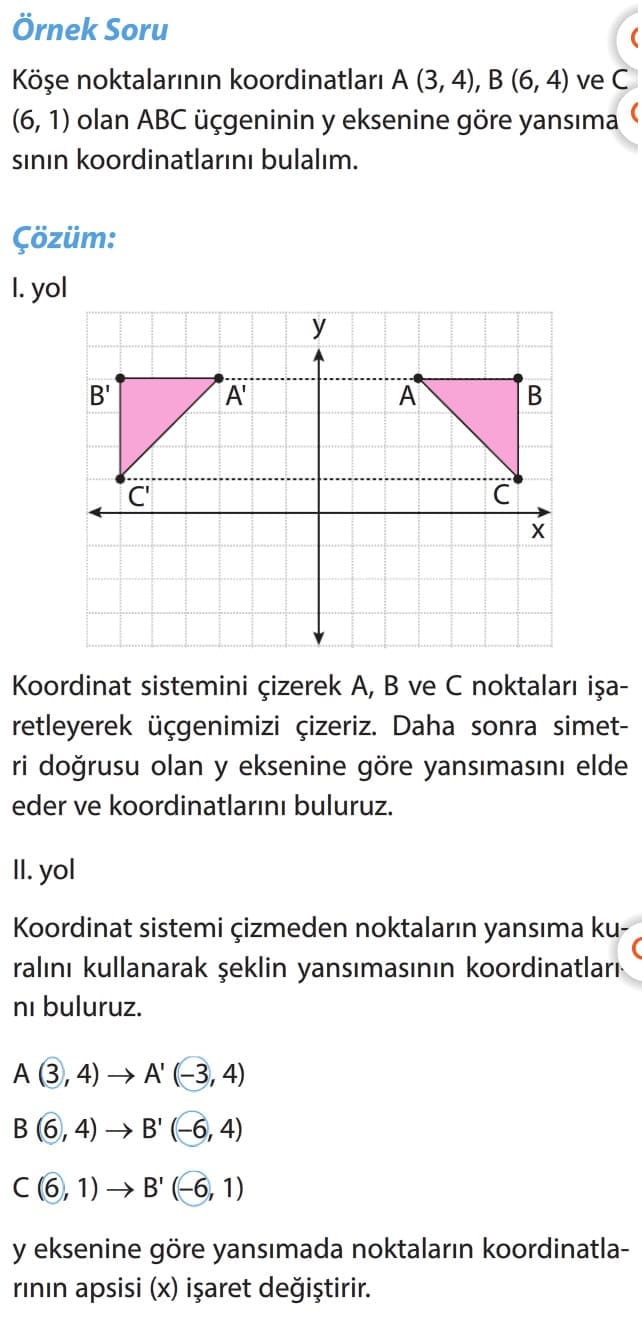
Örnek Soru: Köşe noktalarının koordinatları A (3, 4), B (6, 4) ve C (6, 1) olan ABC üçgeninin y eksenine göre yansıma sının koordinatlarını bulalım.
Çözüm: I. yol
Koordinat sistemini çizerek A, B ve C noktaları işaretleyerek üçgenimizi çizeriz. Daha sonra simetri doğrusu olan y eksenine göre yansımasını elde eder ve koordinatlarını buluruz.
II. yol
Koordinat sistemi çizmeden noktaların yansıma kuralını kullanarak şeklin yansımasının koordinatlarını buluruz. y eksenine göre yansımada noktaların koordinatlarının apsisi (x) işaret değiştirir.